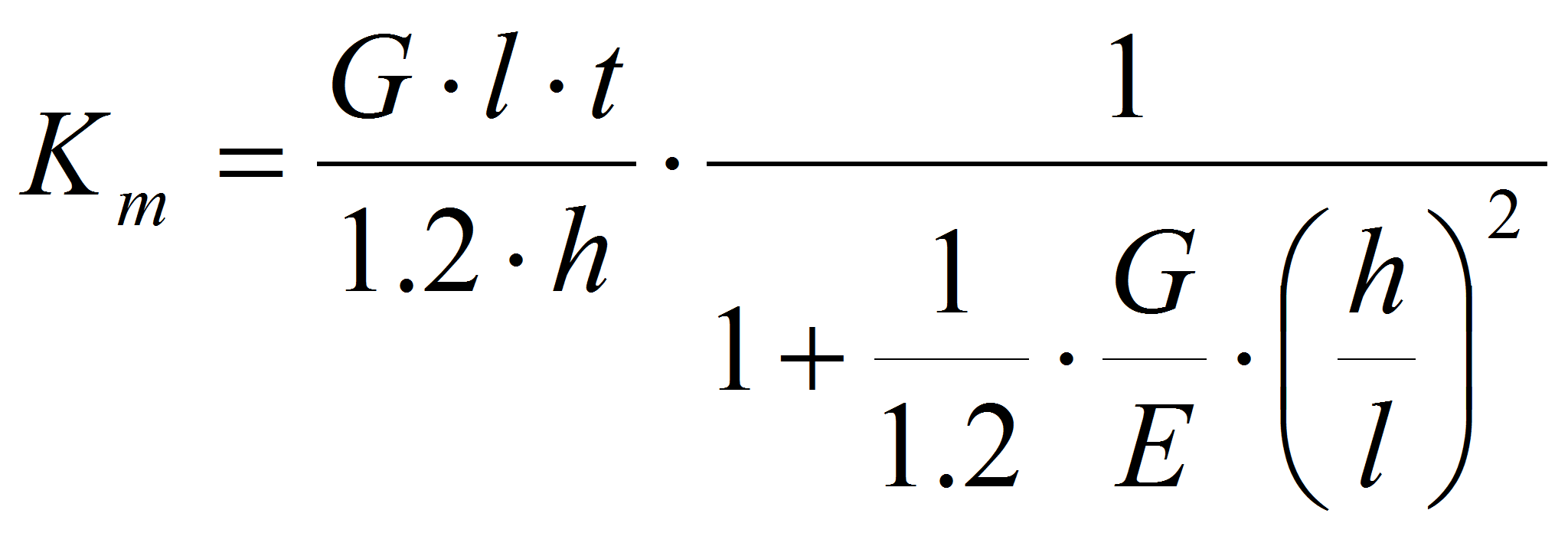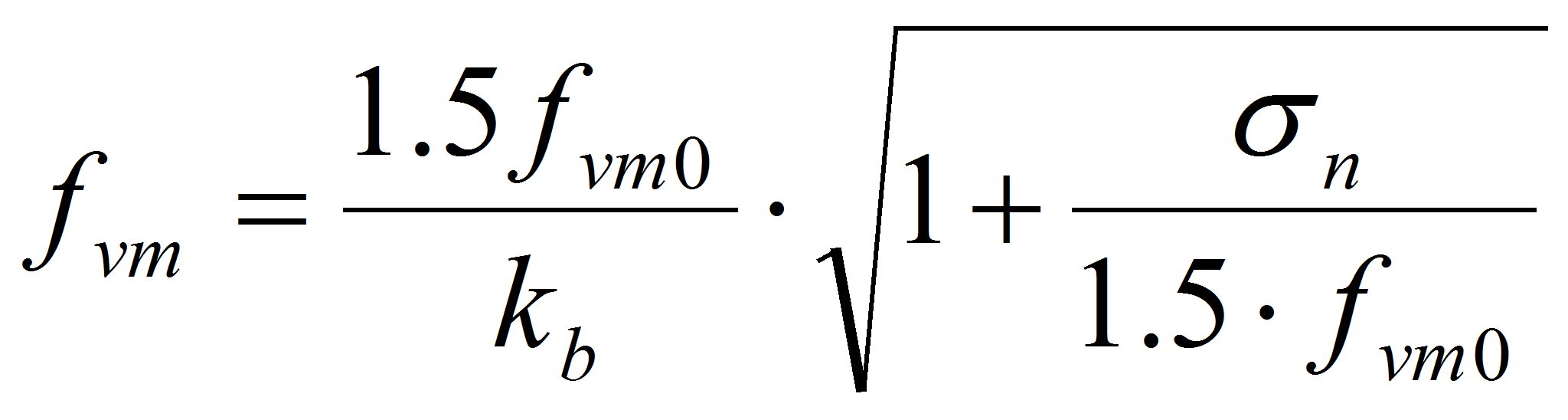Modellazione ed analisi sismica
Il modello di calcolo assume come elementi resistenti all'azione sismica i maschi murari o setti, che corrispondono alle porzioni di muratura comprese fra due aperture successive o fra una apertura e un nodo d’incrocio.
Ipotesi di base della modellazione sismica
Si assumono due ipotesi di base:
- che i maschi abbiano un comportamento di tipo shear-type (ovvero con rotazioni al piede e in testa impedite),
- che gli spostamenti in pianta siano descrivibili come roto-traslazione rigida.
La prima ipotesi è generalmente accettabile ai fini tecnici quando sussiste fra le pareti un sufficiente grado di ammorsamento tale da garantire un comportamento scatolare dell'insieme. In queste condizioni infatti, la presenza dei muri trasversali limita notevolmente la rotazione delle sezioni terminali delle murature, rendendo plausibile l'ipotesi di rotazioni impedite al piede e in testa. Inoltre, nel caso di setti adiacenti ad aperture, la deformabilità del collegamento può essere messa in conto, come in effetti si fa in Por 2000, attraverso un appropriato trattamento del nodo a dimensione finita.
Per quanto riguarda la seconda ipotesi, questa non discende, come pure a volte semplicisticamente si dice (mutuando dal caso degli edifici in c.a.), dalla presenza di solai di piano sufficientemente rigidi da impedire la deformazione in pianta della struttura (la rigidezza dei solai, anche se realizzati in laterocemento, resta irrisoria rispetto a quella della muratura portante) ma è conseguenza anch'essa del comportamento scatolare dell'edificio. Infatti, se i muri sono validamente ammorsati negli incroci, possiamo assimilare la pianta di un edificio murario ad una sezione pluriconnessa, dotata quindi di una forte rigidezza torsionale. In questo contesto, anche in assenza di solai, la risposta ad una spinta orizzontale lungo un setto non produce effetti solo locali, ma porta ad una collaborazione dell'insieme dei setti, che si manifesta con una roto-traslazione dell'insieme, e pertanto gli spostamenti in pianta risultano tali da poter essere decritti con buona approssimazione tramite un moto rigido del solaio.
- La validità di entrambe le ipotesi resta ovviamente legata ad un pieno ammorsamento agli incroci murari ed ad una corretta realizzazione delle aperture, ma questi sono prerequisiti essenziali che una costruzione muraria deve comunque garantire. In tal caso le ipotesi forniscono un buon compromesso fra semplicità di analisi ed accuratezza di modellazione e sono accettabili ai fini tecnici, specie se si considera anche il livello delle approssimazioni coinvolte negli altri aspetti della modellazione (identificazione dei parametri elastici e di resistenza delle murature, valutazione dello stato di degrado ed altro). Si può anche osservare che, all'estremo opposto, una modellazione apparentemente più sofisticata, che veda pareti separate trattate come strutture intelaiate, porterebbe a trascurare del tutto gli effetti legati alla rigidezza torsionale della cassa muraria, con ciò perdendo l'aspetto forse più importante del comportamento della struttura.
Modellazione delle fasce
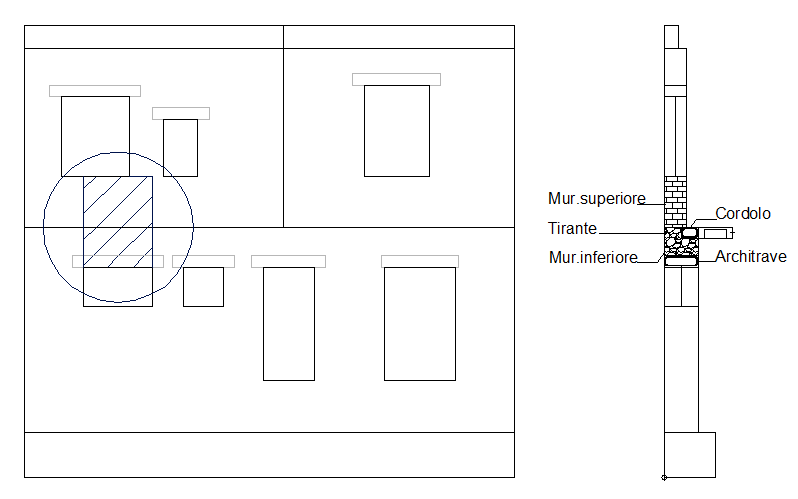
A partire dalla versione V12 il programma consente la modellazione delle fasce ovvero di quelle porzioni di muratura collocate al di sopra di una apertura ed assimilabili a travi in muratura fra due setti murari consecutivi. La configurazione geometrica dell’elemento può essere molto variabile, essendo composta dalla porzione sopra-finestra del piano inferiore e dalla porzione sottofinestra del piano superiore, che in generale possono presupporre diversità di materiale e spessori. Ma oltre a queste, la fascia può comprendere il cordolo di piano, l’architrave dell’apertura e l’effetto di tirantature presenti.
|
|
Per la modellazione delle fasce il programma contempla le due possibilità:
- fasce non modellate:
in questo caso si assume che le fasce siano caratterizzate da resistenza e duttilità piuttosto alte, tali da non avere influenza nella risposta sismica dei setti, che in questo caso sono considerati strettamente nello schema statico sheartype; - fasce modellate:
in questo caso si assume che le fasce siano caratterizzate da resistenza e duttilità finite, tali da influenzare la risposta sismica dei setti, che in questo caso si discostano dallo schema statico sheartype e mostrano un certo grado di rilassamento del vincolo rotazionale in testa, nella misura stabilita dal concomitante effetto flangia dato dalla connessione negli incroci.
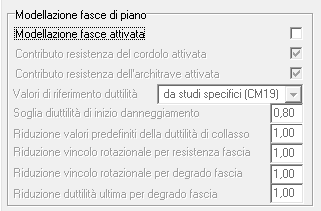
L’attivazione della modellazione delle fasce si fa nella sezione Sismici del foglio delle Opzioni di analisi.
|
|
Se la modellazione delle fasce non viene attivata, si ottiene un modello di calcolo analogo a quelle delle versioni precedenti alla V12.
Se la modellazione delle fasce viene attivata, diventano attivi i relativi parametri di modellazione che consentono di tener conto del contributo del cordolo e dell’architrave, di riferire i valori di duttilità a studi più o meno conservativi e di modulare gli effetti di rilassamento del vincolo rotazionale e del danneggiamento per degrado fascia.
- Modellazione dei maschi murari
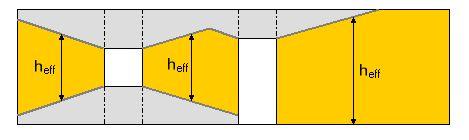
- L'individuazione dei maschi passa attraverso il riconoscimento delle pareti, viste come assemblaggio di uno o più pannelli murari allineati in pianta. In questo contesto la presenza delle aperture, interrompendo la continuità della muratura, indeboliscono la resistenza della parete; ma per contro si osserva, in qualche misura, un aumento di rigidezza nelle immediate vicinanze dei vuoti, dovuto alla presenza delle fasce di piano sopra o sotto l'apertura. Studi sull'argomento modellano tale effetto con una riduzione dell’altezza efficace heff dei maschi posti a lato dell'apertura, tenendo conto di una angolo di diffusione degli sforzi in prossimità dei vuoti (vedasi sull'argomento: Mauro Dolce, "Schematizzazione e modellazione per azioni nel piano delle pareti", Corso sul Consolidamento degli edifici in muratura in zona sismica - Ordine Ingegneri di Potenza)
- L'altezza netta così valutata interviene in sostituzione dell’altezza di piano nel calcolo della rigidezza tagliante e flessionale del setto.
- Nell'ambito della parete, inoltre, è frequente trovare setti adiacenti non intercalati da una apertura. E' questo il caso dei setti a cavallo di un nodo di incrocio o di due setti in contatto, distinti per diversità di spessore o di materiale. Se si ipotizza che durante la deformazione non insorgano distacchi fra i due setti adiacenti (fatto plausibile per l’irrigidimento conferito dai solai), ovvero che l'insieme dei due setti mostri un comportamento solidale, è necessario amplificare in maniera opportuna le rigidezze flessionali dei singoli setti per tener conto del comportamento d'insieme. Questo aspetto di modellazione viene affrontato dal programma e risolto con l'omogeneizzazione delle rigidezze flessionali dei maschi riconosciuti in contatto.
- Comportamento meccanico del maschio murario
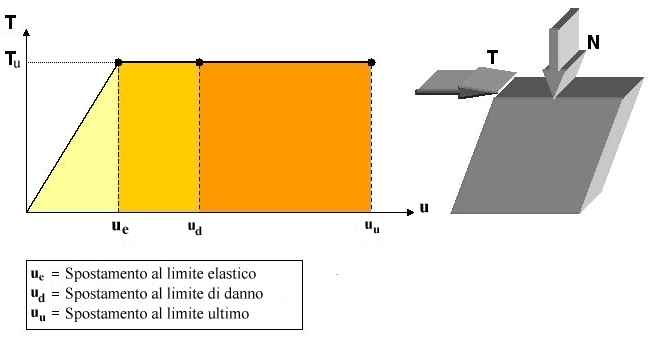
- Si suppone inoltre che l'elemento resistente abbia un comportamento elastico perfettamente plastico, definito da una resistenza ultima (a taglio e a pressoflessione longitudinale) e dai valori limite di deformazione (duttilità di danno, duttilità ultima). Nel seguito, verranno discussi con maggiore dettaglio i termini di resistenza e duttilità che definiscono il legame elasto-platico, in funzione delle indicazioni di normativa.
|
|
|
|
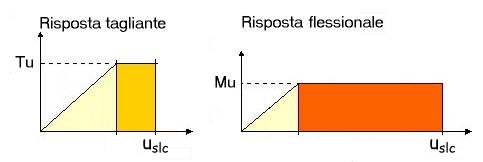
- In virtù del comportamento elasto-plastico assunto per il maschio, la proporzionalità fra sforzo e spostamento è valida soltanto in campo elastico attraverso il valore calcolato di rigidezza, ossia fin tanto che lo spostamento u, dipendente sia dall’intensità della forza orizzontale applicata, sia dalle caratteristiche elastiche del setto di muratura, si mantiene inferiore allo spostamento al limite elastico ue. Oltre detto limite, entrando in campo fessurativo, la muratura dissipa energia sotto forma di deformazione plastica senza più rispettare la legge di proporzionalità forza-spostamento, ma bloccando la portanza raggiunta al limite superiore di resistenza, identificato nel valore del taglio ultimo Tu.o del momento Mu.
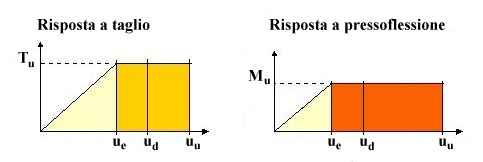
- In funzione dei rapporti esistenti fra le resistenze Tu.e Mu, col progredire del processo deformativo il maschio arriverà al valore limite di resistenza per pressoflessione o per taglio. Da questo punto in poi, continua ad offrire la portanza limite raggiunta, finchè lo spostamento non raggiunge la soglia ultima, al di sopra della quale il maschio è dichiarato collassato e il suo contributo si annulla.
- Rigidezza del maschio murario
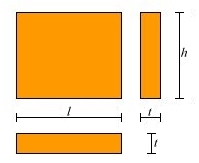
- La rigidezza di un maschio murario, nelle condizioni di rotazioni impedite al piede e in testa, si valuta in base alla teoria della trave deformabile a taglio e a flessione. In particolare, per un maschio di lunghezza l, altezza netta h e spessore t, il valore della rigidezza può essere determinato in base alla formula
|
|
|
Comportamento meccanico delle fasce
Si suppone che le fasce abbiano un comportamento elastico perfettamente plastico (analogo a quello dei setti), definito da una resistenza ultima (a taglio e a pressoflessione longitudinale) e dai corrispondenti valori ultimi di deformazione.
La modellazione delle fasce coinvolge due aspetti distinti: il primo riguarda l’accertamento del vincolo rotazionale che la fascia è in grado di conferire al maschio sottostante, il secondo gli effetti di danneggiamento dovuti al degrado delle fascia sugli elementi ad essa collegati.
Valori resistenti
La fascia è un elemento piuttosto complesso da modellare in quanto oltre alle difficoltà di ordine geometrico connesse con l’eventuale disallineamento delle aperture fra il livello inferiore e superiore, possono coesistere anche diversità di materiale e spessore e i contributi di eventuali architravi, cordoli e tiranti.
Per trattare questi aspetti nel programma si adottano le seguenti formule generalizzate:
Tu = fvmo,i hi ti + fvmo,s hs ts + Vt,cor + Vt,arc taglio ultimo resistente
Mu = Hp ho/2 (1- Hp/(0.85 fhd,s hs ts + 0.85 fhd,i hi ti )) momento ultimo resistente
in cui:
hi ti hs ts altezza e spessore della parte di sezione in muratura afferente al livello inferiore/superiore,
fvmo,i fvmo,s resistenza di progetto a taglio in assenza di compressione della muratura inferiore/superiore,
Vt,cor Vt,arc resistenza di progetto a taglio del cordolo e dell’architrave,
ho altezza della sezione complessiva omogeneizzata, ovvero: ho = (hs ts + hi ti)/ ti
fhd,i fhd,s resistenza di progetto a compressione orizzontale della muratura inferiore,
che in via approssimata può essere assunta pari a a quella in direzione verticale.
Hp min(Het, Hmu) in cui:
Het capacità a trazione dell’elemento teso disposto orizzontalmente,
Hmu capacità a trazione dovuta al meccanismo di ingranamento dei blocchi di muratura,
Hmu = min(fbt/2, 0.40 fhd,i hi ti ) + min(fbt/2, 0.40 fhd,s hs ts )
in cui:
fbt resistenza a trazione dei blocchi in direzione orizzontale,
un valore approssimato è indicato in C8.7.1.3.1.1/Ntc18:
fbt= 0.1 fb
essendo fb la resistenza a compressione dei blocchi in direzione orizzontale.
Nel caso di analisi pushover le resistenze sono assunte nel loro valore medio.
Limiti di duttilità
I limiti di duttilità della fascia sono espressi in rapporto alla sua luce, facendo riferimento a due fonti principali, che il progettista può selezionare nel foglio delle Opzioni di Analisi:
- i più recenti studi sperimentali sulle fasce (Beyer, Cattari, Mangalathu e altri), recepiti in CM2019,
uSLC = 0,015 - 0.020 a pressoflessione in presenza di elemento resistente a trazione,
uSLC = 0.015. a taglio
- le disposizioni relative ai maschi estese per analogia alle fasce, riportate in Ntc2018:
uSLC = 0,010 - 0.016 a pressoflessione per muratura ordinaria/armata,
uSLC = 0.005 - 0.005. a taglio per muratura ordinaria/armata.
In aggiunta, l’utente può impostare un fattore riduttivo nel caso volesse adottare valori più cautelativi rispetto a quelli predefiniti.
Sollecitazioni agenti nelle fasce
Nel corso dell’analisi pushover vengono costantemente valutate le sollecitazioni di taglio e momento agenti nelle fasce e la duttilità raggiunta in esse in termini di rotazione plastica.
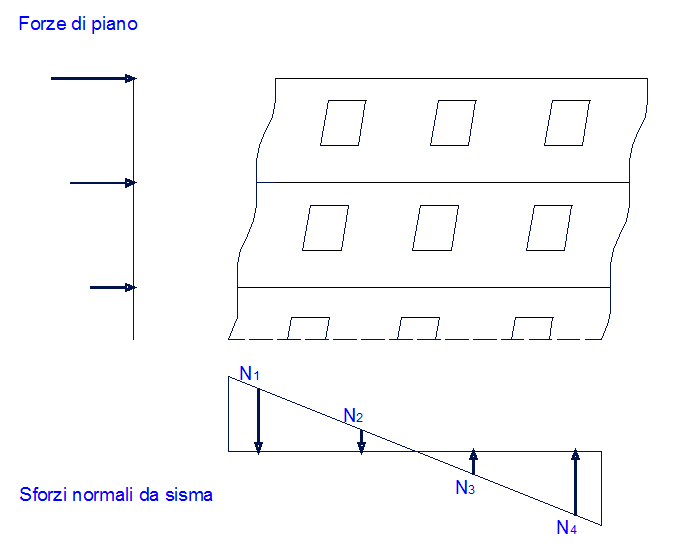
Innanzitutto si determinano per ogni passo di carico la distribuzione degli sforzi normali nei maschi che equilibrano le forze orizzontali sismiche, adottando un modello cinematico tridimensionale che assicuri la congruenza degli spostamenti verticali di punti adiacenti, ma appartenenti a pareti diverse, per tener conto delle connessioni d’angolo fra le pareti, ovvero del cosiddetto effetto flangia, fondamentale nelle strutture in muratura perché è alla base del comportamento scatolare.
|
Schema di equilibrio fra forze sismiche e sforzi assiali |
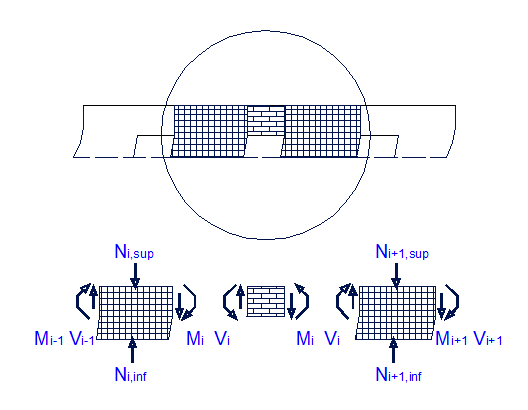
Schema delle sollecitazioni fra fascia e maschi adiacenti |
Noti gli sforzi normali nei maschi è possibile determinare il taglio Vi nella i-esima fascia imponendo l’equilibrio alla traslazione verticale nel maschio che precede la fascia in esame
Il valore del momento all’estremità delle fasce discende dall’equilibrio alla rotazione dell’elemento:
Accertamento del vincolo rotazionale
L’accertamento del vincolo rotazionale può essere valutato in modo semplificato in funzione del rapporto fra la capacità resistente complessiva delle due fasce collegate al maschio e il momento resistente del maschio stesso, tenendo conto quando presenti delle connessioni d’angolo con muri trasversali. In funzione di questo effetto il maschio può subire un effetto di rilassamento del vincolo rotazionale in testa allontanandosi dalla soluzione sheartype.
Effetti del danneggiamento delle fasce
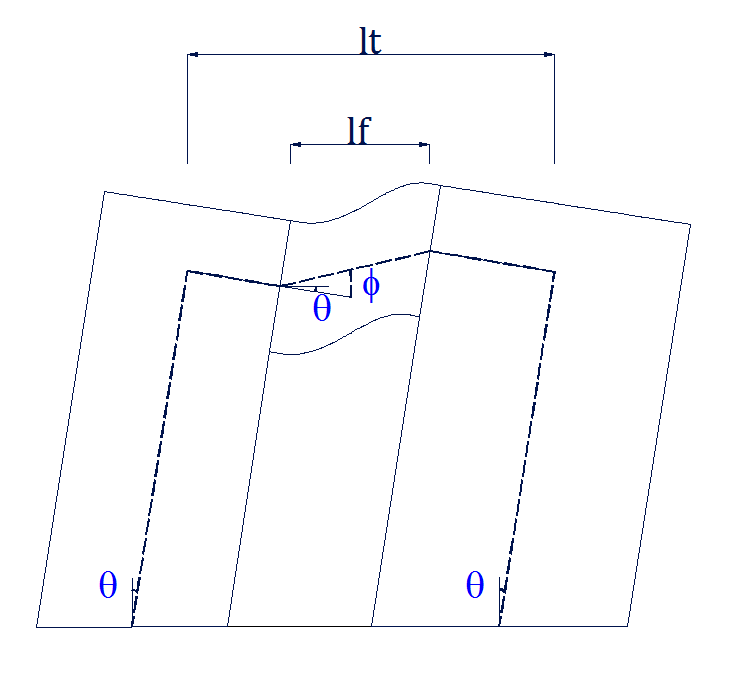
L’effetto dovuto al degrado delle fasce è invece dovuto all’accumulo della deformazione plastica nella fascia misurato con la deformazione angolare ϕ, che può essere messa in relazione con la deformazione angolare dei maschi θ; nell’ipotesi che le porzioni dei pannelli lateralmente alla fascia mostrino un comportamento rigido e che la deformazione si concentri tutta nella fascia:
ϕ = θ lt / lf
in cui lt e lf sono rispettivamente luce fra gli assi dei maschi e la luce della trave di muratura.
|
Deformata elastoplastica di un portale murario |
Nel corso dell’analisi pushover è possibile quindi controllare la deformazione della fascia, comparando il drift raggiunto al passo con i valori limiti di collasso assunti per l’elemento, in funzione delle impostazioni eseguite nelle Opzioni di Analisi. Il collasso è raggiunto la prima volta che la fascia raggiunge la duttilità limite impostata. Gli effetti del degrado della fascia sono applicati come danneggiamento degli elementi maschi ad essa collegati in due modalità distinte e cumulabili:
- in termini di degrado del vincolo rotazionale in testa ai maschi con conseguente calo di resistenza,
- in termini di riduzione della duttilità di collasso dei maschi.
In entrambi i casi gli effetti sono regolabili con i due parametri a discrezione del progettista, variabili con continuità da 0 a 1:
- fattore riduttivo del degrado rotazionale: 0=effetto nullo, 1=effetto predefinito,
- fattore riduttivo del degrado duttilità: 0=effetto nullo, 1=effetto predefinito.
In termini di modalità l’effetto del degrado della fascia può essere applicato:
- in modo pressoché concentrato in prossimità del collasso,
- in modo distribuito a partire da una soglia predefinita di duttilità.
- Resistenza e duttilità della muratura
- Generalmente gli edifici in muratura sono costituiti da elementi con caratteristiche diverse per geometria, rigidezza, duttilità e resistenza e pertanto si comportano in maniera altrettanto diversa allorché sottoposti a sforzo da parte dei carichi agenti.
- Ciascun setto di muratura potrà tollerare valori limitati sia di sforzo che di deformazione e il modo attraverso cui resiste alle sollecitazioni dipende fortemente da queste caratteristiche.
- In particolare, all’attingersi del massimo sforzo sopportabile, le risorse meccaniche si traducono nella capacità di assorbire energia per deformazione plastica, ed è proprio in questa fase che la muratura preserva la struttura dal repentino collasso fragile, giacché la quantità di energia dissipabile in campo plastico è spesso paragonabile, se non superiore, a quella che viene consumata in campo elastico.
- D’altra parte anche le risorse in campo plastico evidenziano un limite, raggiunto il quale il setto è da considerare collassato e, non essendo più in grado di equilibrare i carichi esterni, deve essere escluso dall’insieme murario ancora resistente.
- Risposta flessionale e a taglio dei maschi per analisi secondo Ntc08/18
- I maschi murari sono caratterizzati da un comportamento bilineare elastico-perfettamente plastico, con resistenza equivalente al limite elastico e spostamenti al limite elastico ed ultimo definiti sia per la risposta flessionale, sia per la risposta a taglio.
- Taglio ultimo longitudinale per murature con tessitura regolare
- Il valore del taglio ultimo resistente si ottiene dalla seguente formula
- Tu = (fvmo+ tanφ σn) L B
- in cui:
- L, B lunghezza e spessore del maschio murario (dimensioni in pianta),
- fvmo resistenza tangenziale media della muratura fvmo= fvk0/0.7
- fvk0 resistenza tangenziale caratteristica assegnata alla muratura
- φ angolo di resistenza a taglio della muratura (valore consigliato tanφ=0.4)
- σn tensione normale media, prodotta dal carico verticale e dalle precompressioni.
- Taglio ultimo longitudinale per murature con tessitura irregolare
- Il valore del taglio ultimo resistente si ottiene dalla seguente formula
- Tu = fvm L B
- in cui:
L, B lunghezza e spessore del maschio murario (dimensioni in pianta),
fvm resistenza tangenziale media della muratura ottenuta come:
fvm0 resistenza tangenziale media di calcolo per carico verticale nullo
fvm0= fvk0/(0.7*γc)
γc fattore riduttivo per le resistenze (fattore di confidenza),
kb coefficiente correttivo legato alla distribuzione degli sforzi sulla sezione
kb = H/L, con valori limitati nel range 1≤ kb ≤ 1.5
fvk0 resistenza tangenziale caratteristica assegnata alla muratura
σn tensione normale media, prodotta dal carico verticale e dalle precompressioni.
- Momento ultimo longitudinale
- Il valore del momento ultimo resistente si ottiene dalla seguente formula
- Mu = (L2 B σn/2) (1- σn/(0.85 fd))
- in cui:
- L, B lunghezza e spessore del maschio murario,
- fd resistenza normale di calcolo della muratura,
fd = fk/γc
- fk resistenza normale caratteristica assegnata alla muratura
- γc fattore riduttivo per le resistenze (fattore di confidenza),
- σn tensione normale media.
- Nel caso di murature rinforzate con intonaco armato o compositi fibrorinforzati si tiene conto del contributo a trazione offerto dall’armatura o dalle fibre.
- Limiti di duttilità
- Nell'ambito di un modello elastico-perfettamente plastico del setto murario, i limiti di duttilità determinano i valori di spostamento in corrispondenza dei quali si assume venga raggiunto un particolare stato limite: di danno, di collasso a taglio o di collasso a flessione. I limiti di duttilità vengono espressi in rapporto all'altezza di calcolo del setto, secondo le seguenti tabelle, in funzione della a norma adottata.
Limiti di duttilità dei setti secondo Ntc08
|
|
Tipo di muratura |
||
|
|
Ordinarie esistenti |
Ordinarie nuove |
Armate |
|
duttilità l. di operatività |
0.003 h *2/3 §7.3.7.2 |
0.003 h *2/3 §7.3.7.2 |
0.004 h *2/3 §7.3.7.2 |
|
duttilità l. di danno |
0.003 h §7.3.7.2 |
0.003 h §7.3.7.2 |
0.004 h §7.3.7.2 |
|
duttilità l. ultimo a taglio |
0.004 h C8.7.1.4 |
0.004 h §7.8.2.2 |
0.006 h §7.8.3.2 |
|
duttilità l. ultimo a p.flessione |
0.006 h C8.7.1.4 |
0.008 h §7.8.2.2 |
0.012 h §7.8.3.2 |
Limiti di duttilità secondo Ntc18
|
|
Tipo di muratura |
||
|
|
Ordinarie esistenti |
Ordinarie nuove |
Armate |
|
duttilità l.operatività |
0.002 h *2/3 §7.3.6.1 |
0.002 h *2/3 §7.3.6.1 |
0.003 h *2/3 §7.3.6.1 |
|
duttilità l. di danno |
0.002 h §7.3.6.1 |
0.002 h §7.3.6.1 |
0.003 h §7.3.6.1 |
|
duttilità l. ultimo a taglio |
0.005 h (f.diag/m.irr.) §C8.7.1.3.1.1 0.005 h (t.scor/m.reg/b.pieni) §C8.7.1.3.1.1 0.004 h (t.scor/m.reg/b.forati) §C8.7.1.3.1.1 |
0.005 h §7.8.2.2 |
0.008 h §7.8.2.3 |
|
duttilità l. ultimo a p.flessione |
0.010 h §C8.7.1.3.1.1 |
0.010 h §7.8.2.2 |
0.016 h §7.8.2.3 |
Sebbene nella normativa non si faccia menzione di fattori di sicurezza da applicare ai valori tabellati sopra, il programma consente la possibilità di applicare un fattore di sicurezza (maggiore o uguale ad uno) che possa tener conto di probabili effetti sfavorevoli all'estrinsecarsi della duttilità, come ad esempio per localizzazione delle deformazioni o per danneggiamenti già esistenti (vedi § Duttilità limiti, Capitolo 4).
- In particolare, i valori di calcolo delle duttilità limiti si ottengono come:
- dD = dkD /γd duttilità limite di danno,
- dU = μkU /γd duttilità limite ultima al collasso,
- in cui:
- dkD e dkU sono le duttilità limite (di danno e ultima) assegnati per il tipo di muratura,
- γd è il fattore di sicurezza sulle duttilità assegnato (γd ≥ 1).
- Risposta flessionale e a taglio dei maschi per analisi secondo Ntc96
- I pannelli murari sono caratterizzati da un comportamento bilineare elastico-perfettamente plastico, con resistenza equivalente al limite elastico e spostamenti al limite elastico ed ultimo definiti mediante al risposta a taglio.
- Taglio ultimo longitudinale
- Il valore del taglio ultimo resistente si ottiene dalla seguente formula
- Tu = τu L B
- in cui:
- L e B sono lunghezza e spessore del maschio murario (dimensioni in pianta),
- τu è la resistenza tangenziale ultima calcolata secondo Turnsek e Cacovic.
- Limiti di duttilità
- Spostamento al limite di fessurazione: uf = ue(1+df)
- Spostamento al limite ultimo: uu = ue(1+du)
- in cui:
- ue è lo spostamento al limite elastico,
- df è la duttilità di fessurazione assegnata alla muratura,
- du è la duttilità ultima assegnata alla muratura.
- Tensione tangenziale ultima secondo Turnsek e Cacovic
- Riportiamo per completezza la formula della tensione tangenziale ultima secondo gli autori Turnsek e Cacovic:
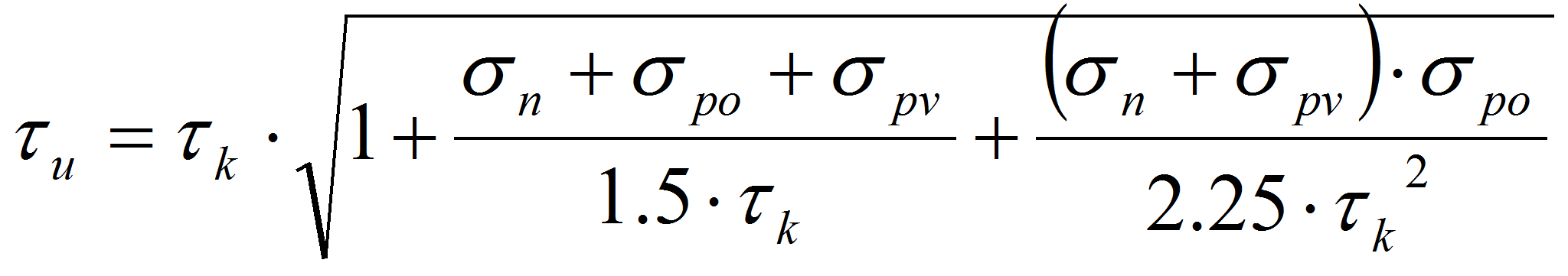
- in cui:
- τk è la resistenza tangenziale caratteristica assegnata alla muratura (fvk0),
- σn è la tensione normale media,
- σpo è la tensione normale dovuta a precompressioni orizzontali,
- σpv è la tensione normale dovuta a precompressioni verticali.