ll metodo delle strisce
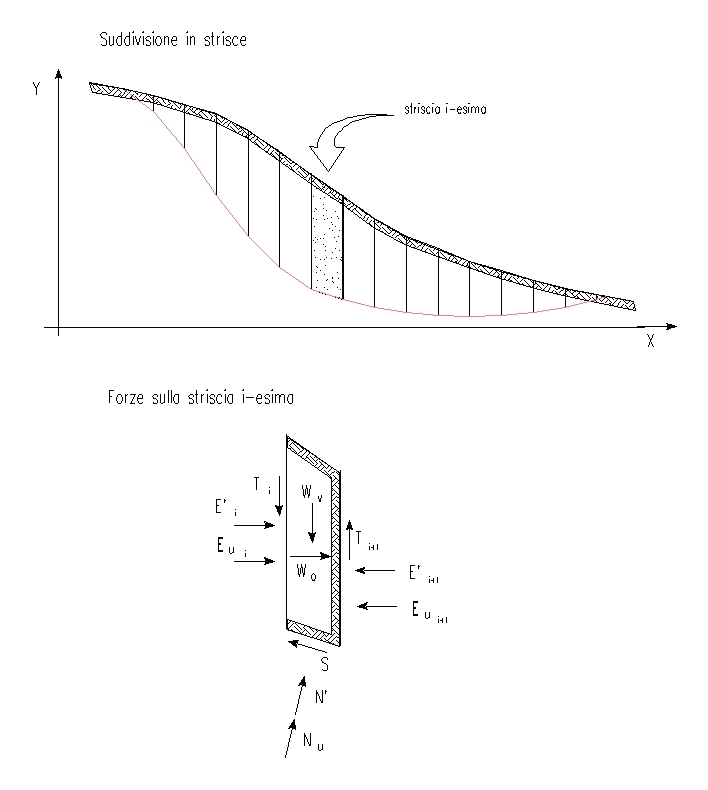
Per tener conto in modo semplice ma sufficientemente accurato dell'andamento variabile delle tensioni lungo la superficie di scivolamento, l'intero pendio viene suddiviso in un insieme opportunamente fitto di strisce verticali come indicato in figura.
Le forze agenti sulla striscia
La generica striscia è sottoposta ad un sistema di forze derivanti dalle azioni interne (peso proprio ed eventuale carico sismico) e dalle azioni di contatto agenti sul piano di campagna, sulle due interfacce (di sinistra e di destra) che la collegano alle strisce adiacenti e sulla parte della superficie di scivolamento tagliata dalla striscia.
Con riferimento alla figura ed assumendo uno spessore trasversale unitario, possiamo distinguere:
- Wv Carico verticale totale sulla striscia (peso proprio, carichi agenti sul piano di campagna ed eventuali altre forze note);
- Wo Carico orizzontale totale (azione sismica, effetto di tiranti ed altro);
- E' Risultante delle tensioni normali effettive sull'interfaccia:
- Eu Risultante delle tensioni neutre sull'interfaccia;
- T Risultante delle tensioni tangenziali sull'interfaccia;
- N' Risultante delle tensioni normali effettive agenti lungo la superficie di scivolamento;
- Nu Risultante delle tensioni neutre agenti lungo la superficie di scivolamento;
- S Risultante delle tensioni tangenziali agenti lungo la superficie di scivolamento.
I termini noti
Le risultanti dei carichi Wv e Wo,e le risultanti delle tensioni neutre Eu ed Nu sono in generale note sia in intensità che in posizione (sono infatti o direttamente definite o facilmente calcolabili dai dati del problema).
I termini incogniti
Tutte le altre sono da considerare incognite sia in termini di intensità che di posizione. Per l'intero pendo, che pensiamo suddiviso in n strisce, abbiamo così le seguenti variabili:
- n-1 risultanti normali E' agenti sulle (n-1) interfacce;
- n-1 risultanti tangenziali T agenti sulle (n-1) interfacce;
- n risultanti normali N' agenti sulle n intercette della superficie di scivolamento;
- n risultanti tangenziali S agenti sulle n intercette della superficie di scivolamento;
- n-1 ascisse di applicazione delle forze orizzontali E';
- n ascisse di applicazione delle forze normali N';
- 1 fattore di sicurezza F del pendio.
per un totale quindi di (6n - 2) incognite.
Le equazioni disponibili
D'altra parte, per ciascuna delle n strisce del pendio, possiamo scrivere tre equazioni di equilibrio di corpo rigido (in direzione orizzontale, verticale ed alla rotazione) ed una condizione di Mohr-Coulomb.
Il problema sotto determinato
Il problema, così caratterizzato da 4n equazioni e (6n-2) incognite, risulta ovviamente sottodeterminato e richiede pertanto (2n-2) assunzioni indipendenti per poter essere risolto in modo univoco.