Si parte assumendo una distribuzione di accelerazioni, il più possibile rappresentativa del campo di accelerazioni indotto dal sisma. Indicando con w la forma modale e con ag il valore di riferimento dell'accelerazione sismica al suolo, il sistema di forze inerziali indotto sulla struttura è determinato dalla relazione:


essendo M la matrice delle masse della struttura e p il fattore di partecipazione definito dalla:

dove i corrisponde ad un moto rigido unitario nella direzione dell'eccitazione sismica.

Si esegue una analisi statica nonlineare al passo assumendo la struttura soggetta ad un sistema di forze {a, f}, per incrementi successivi del parametro amplificativo a fino al collasso ultimo della struttura, tenendo conto sia dell'insorgenza di deformazioni plastiche che del degrado di resistenza negli elementi della struttura indotto da deformazioni eccessive. Come risultato si ottiene una successione di configurazioni di equilibrio {ag, u}, che possono essere raccolte in una curva di equilibrio 

ag = ag(u)


dove u è il valore scalare dello spostamento di riferimento, convenientemente definito dalla relazione 

Ora, se osserviamo la precedente espressione, vediamo che il valore dello spostamento di riferimento viene calcolato con una equivalenza energetica col lavoro di deformazione (spostamento = lavoro/forza). Questa modalità di calcolo ha il vantaggio di rendere i risultati di analisi indipendenti dalla scelta arbitraria del punto di controllo e dalle irregolarità in altezza della costruzione, dovute ad esempio alla presenza di torrini o di piani di copertura inclinati o sfalsati. Il valore che si ottiene può essere visto come uno spostamento medio, in termini energetici, e come tale è minore (o al limite uguale) allo spostamento massimo di piano. Considerando questo, si può ritenere che la procedura porti ad una stima in sicurezza della capacità di spostamento, rispetto ad una scelta del punto di controllo nel centro di massa dell'ultimo livello. 


Sulla curva di equilibrio sono individuati i punti corrispondenti agli stati limite di interesse:

stato limite elastico [SLE]:

corrisponde al punto in cui ha termine il comportamento elastico lineare;

stato limite di operatività [SLO]:

rappresenta il punto in cui si ha il primo raggiungimento rotazione di snervamento in qualche elemento (opzionale) o il primo raggiungimento dello scorrimento limite di interpiano impostato per questo stato limite (assegnato alla colonna urx dello s.l. SLO nella griglia Stati limite: opzioni delle verifiche, tipicamente pari a 2/3 del valore analogo per SLD) in qualche maglia di telaio (fra quelle marcate);

stato limite di danno [SLD]:

rappresenta il punto in cui si ha il primo raggiungimento della rotazione di snervamento in qualche elemento (opzionale) o il primo raggiungimento dello scorrimento limite di interpiano (assegnato alla colonna urx dello s.l. SLD nella griglia Stati limite: opzioni delle verifiche) in qualche maglia di telaio (fra quelle marcate);

stato limite di salvaguardia vita [SLV]:

rappresenta il punto in cui si ha il primo raggiungimento di una aliquota prefissata (per default il 75%, definibile nel Quadro riassuntivo dell'analisi pushover) della rotazione di collasso θu in qualche elemento o la prima occorrenza di un collasso di tipo fragile, in funzione delle opzioni impostate (superamento della resistenza a taglio negli elementi o nei nodi);

stato limite di collasso [SLC]:

corrisponde ad una caduta di carico pari al 15% del valore massimo raggiunto.


L'osservazione della curva fornisce due informazioni significative del comportamento strutturale: il valore massimo dell'accelerazione sostenuta dalla struttura e l'escursione massima dello spostamento raggiunto. Il primo, considerato in rapporto alla accelerazione agente in corrispondenza al limite elastico, fornisce il cosiddetto rapporto di sovraresistenza che può essere utilizzato, come suggerito nelle norme, ai fini di una migliore caratterizzazione del fattore di struttura q e quindi a migliorare l'affidabilità dell'analisi lineare. La seconda individua, tramite il rapporto tra lo spostamento ultimo e quello al limite elastico, la duttilità complessiva della struttura, anche esso da porre in relazione col fattore di struttura q (valori ridotti della duttilità corrispondono a valori più bassi di q). 


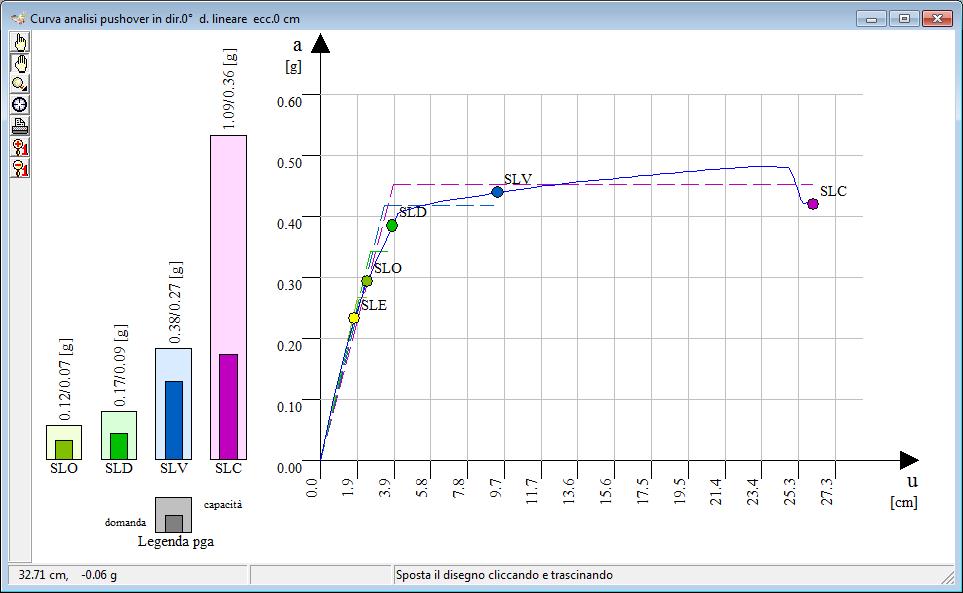
Vista di una curva di equilibrio ottenuta con l’analisi pushover

Verifica della capacità sismica negli stati limite SLO, SLD, SLV e SLC

Gli spostamenti uO, uD, uV e uC raggiunti nei punti limite SLO, SLD, SLV e SLC sono particolarmente significativi per una valutazione della capacità sismica della struttura. E’ infatti possibile condurre una verifica “pushover” per ognuno degli stati limite menzionati, nel modo seguente.


La curva viene semplificata e ridotta a curva bilineare, caratterizzata da una rigidezza equivalente Ke, da una accelerazione equivalente allo snervamento ay. Si viene così a definire un sistema elastoplastico ad un grado di libertà. E' possibile anche caratterizzare la risposta sismica di quest'ultimo attraverso la risposta sismica del sistema elastico corrispondente, di rigidezza Ke e quindi di periodo proprio 

Si è visto infatti, attraverso correlazioni statistiche che, sotto azione sismica, i due sistemi presentano la stessa escursione massima in spostamenti se T > Tc. 

Per T < Tc, l'escursione in spostamento del sistema nonlineare uRN è in generale maggiore di quella del sistema elastico uRE, ma può essere messa in relazione con quest'ultima attraverso la formula:

dove il fattore q* è calcolato in funzione del rapporto tra l'accelerazione spettrale as = ag S(T) e l'accelerazione al limite di snervamento del sistema bilineare equivalente ay 

Lo spostamento richiesto uRN può essere pertanto espresso in funzione dell'accelerazione di riferimento al suolo ag. Eguagliando l'espressione dello spostamento richiesto uRN con gli spostamenti disponibili uL, uS ed uC ai diversi limiti considerati, possono essere pertanto valutate le corrispondenti accelerazioni ammissibili al suolo (Accelerazione di picco al suolo o "pga"). 

Una volta che le accelerazioni al suolo sostenibili per gli stati limite SLD, SLV e SLC siano state calcolate, la verifica si intende soddisfatta se queste risultano maggiori delle corrispondenti accelerazioni al suolo di progetto (accelerazioni richieste), ovvero:

Verifica per s.l. di Operatività (SLO) soddisfatta se                 pgaSLO ≥ ago

Verifica per s.l. di Danno (SLD) soddisfatta se                         pgaSLD ≥ agd

Verifica per s.l. di Salvaguardia Vita (SLV) soddisfatta se                 pgaSLV ≥ agv

Verifica per s.l. di Collasso (SLC) soddisfatta se                         pgaSLC ≥ agc

Le accelerazioni al suolo di progetto ago, agd, agv, agc sono quelle impostate nel foglio Parametri sismici e corrispondono alle accelerazioni di riferimento del sito Ag*, relative ai tre periodi di ritorno dell’azione sismica (per s.l. di danno, per s.l. ultimo, per s.l. di collasso). In termini di probabilità di superamento nella vita di riferimento PVR, si hanno le seguenti corrispondenze:

ago         per s.l. di Operatività (SLO)                 corrispondente alla PVR del 81%,

agd         per s.l. di Danno (SLD)                         corrispondente alla PVR del 63%,

agv         per s.l. di Salvaguardia vita (SLV)                corrispondente alla PVR del 10%,

agc         per s.l. di Collasso (SLC)                 corrispondente alla PVR del 5%.


Nel disegno della curva pushover sono riportati al riguardo tre istogrammi di verifica per i quattro  stati limite SLO, SLD, SLV e SLC, che riportano in grafico le pga sostenibili e quelle richieste e consentono di apprezzare immediatamente il soddisfacimento della verifica.


E' utile ricordare che una valutazione di sicurezza condotta in questo modo soffre fortemente delle assunzioni semplificative fatte, che non sempre trovano un pieno riscontro nella realtà sempre molto complessa ed articolata del comportamento strutturale. L'analisi pushover consente tuttavia di arricchire notevolmente le informazioni ottenute dall'analisi dinamica modale condotta in campo elastico ed insieme a questa fornisce un quadro complessivo utile ad un migliore e più affidabile dimensionamento della struttura. In particolare, permette di valutare, a valle del progetto delle armature, se effettivamente la struttura così progettata soddisfi le caratteristiche di duttilità richieste e quindi se il fattore di struttura utilizzato (assegnato da input) sia adeguato alle effettive risorse di duttilità della struttura.

Implementazione in Edisis

L’implementazione in Edisis dell’analisi statica nonlineare è svolta secondo quanto esposto in precedenza. Sono considerati i seguenti carichi:

  • Carichi permanenti (assunti costanti nell’analisi)
  • Carichi termici, affetti dal fattore di combinazione Ψ2 (assunti costanti nell’analisi)
  • Carichi variabili statici, Ψ2 (assunti costanti nell’analisi)
  • Azioni statiche agf, prodotte da una distribuzione di accelerazioni sismiche orizzontali, proporzionalmente crescenti.

L'analisi è ripetuta per valori diversi dell’angolo di incidenza sismico, e per diverse distribuzioni di accelerazioni (costante o lineare lungo l’altezza).

All’attivazione dell’analisi, compare una finestra in cui vengono assegnati i parametri necessari. Questi ultimi sono inizializzati con valori di default ma possono essere variati dall’utente in relazione a esigenze specifiche.

Le rotazioni al limite di snervamento e al collasso sono inoltre valutate secondo le indicazioni fornite dalle Ntc18, come riportato nei seguenti paragrafi.

Avvio dell'analisi con la soluzione quasi-permanente

I primi tre punti del precedente elenco corrispondono nell'insieme alla cosiddetta soluzione QP (quasi-permanente), ovvero alla combinazione di carichi permanenti e variabili associati alla presenza del sisma. In effetti nel primo passo dell'analisi si valuta il grado d'impegno rispetto alla sola soluzione QP, ovvero senza sisma. Considerato che il modello strutturale è a comportamento elasto-plastico, tutti gli elementi sono a resistenza limitata. In strutture fortemente sottodimensionate o degradate, questo fatto può  determinare  difficoltà nell'equilibrio dei carichi esterni, nel senso che la struttura nelle condizioni in cui si trova potrebbe essere nell'impossibilità di sostenere i carichi quasi-permanenti, ovvero incorrere in un meccanismo di crisi ancora prima che venga applicata una sepur minima azione sismica. In queste condizioni, è impossibile determinare il limite elastico, che per definizione corrisponde al moltiplicatore λ del carico sismico che porta alla prima occorrenza del raggiungimento del limite di resistenza in qualche elemento. L'analisi incrementale perde così di significato e non può essere eseguita. Queste situazioni però sono riconosciute dal programma nello step iniziale dell'analisi pushover e sono opportunamente segnalate con opportuni messaggi di avvertimento:

  • "Attenzione: grave insufficienza di resistenza per carichi statici. Impossibile eseguire l'analisi sismica non lineare.Impegno massimo: "
    In questo caso l'insufficienza è giudicata grave ed è impossibile procedere con l'analisi pushover.
  • "Attenzione: insufficienza di resistenza per carichi statici. Impegno massimo: "
  • In questo caso l'insufficienza è meno grave del caso precedente e consente l'innesco dell'analisi pushover, anche se il processo può soffrire del mal condizionamento iniziale.

Rotazione limite di snervamento

Per la valutazione della rotazione limite di snervamento θy si fa riferimento alle seguenti espressioni: 

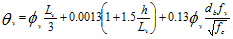               per travi e pilastri 

Per i riferimenti di normativa vedi: Ntc18-C8.7.2.7.a, Istruzioni Ntc08-8.7.2.1 a, Opcm 3274-11.1a.


               per pareti 

Per i riferimenti di normativa vedi: Ntc18-C8.7.2.7.b, Istruzioni Ntc08 p. 8.7.2.1 b, Opcm 3274-11.1b.


in cui:

Lv         luce di taglio, ovvero distanza fra la sezione di estremità e quella a momento nullo,

ϕy         curvatura a snervamento della sezione terminale,

h         altezza della sezione,

db        diametro medio delle barre longitudinali,

fc        resistenza a compressione del calcestruzzo                 [espresso in Mpa],

fy        resistenza a snervamento dell’acciaio longitudinale         [espresso in Mpa].

Rotazione limite di collasso

Per la valutazione della rotazione limite a collasso θu si fa riferimento alla seguente espressione: 

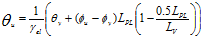
Per i riferimenti di normativa vedi:  Ntc18-C8.7.2.5, Opcm 3274-11.A.3, Istruzioni Ntc08-C8F.5.


in cui:

γel         fattore riduttivo di duttilità (pari a 1.5 per elementi primari e ad 1.0 per elementi secondari) [Ntc18-C8.7.2.3.2]

θy        rotazione rispetto alla corda allo snervamento

ϕu         curvatura ultima valutata considerando le deformazioni ultime del conglomerato         
               (tenuto conto del confinamento) e dell’acciaio 

ϕy         curvatura a snervamento valutata considerando l’acciaio alla deformazione di snervamento 

Lv         luce di taglio, ovvero distanza fra la sezione di estremità e quella a momento nullo,

LPL         lunghezza di cerniera plastica, valutabile come [Ntc18-C8.7.2.3.2]:

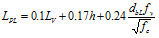
in cui:

h         altezza della sezione,

dbL        diametro medio delle barre longitudinali 

fc        resistenza a compressione del calcestruzzo [Mpa],

fy        resistenza a snervamento dell’acciaio longitudinale [Mpa],

fyw        resistenza a snervamento dell’acciaio trasversale.


La deformazione ultima del calcestruzzo confinato si valuta con la seguente espressione:

in cui:

ε*cu        deformazione ultima del calcestruzzo confinato

εcu        deformazione ultima del calcestruzzo adottata per le verifiche slu (tipicamente 0.0035)

ρs        percentuale di armatura trasversale                ρs = nb Ast /bo sh

sh        interasse delle staffe nella zona critica,

nb         numero di bracci staffe,

Ast        area trasversale del tondino staffa,

α        fattore di efficienza del confinamento  [Ntc18-C8.7.2.3.2]:

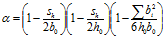
b0h0         base ed altezza del nucleo confinato,

bi        distanze delle barre longitudinali trattenute da tiranti o staffe presenti sul perimetro.

Riduzione per carenza di dettagli sismici

Nel caso l'elemento resistente non sia dotato di adeguati dettagli di tipo antisismico, ossia non rispetti le percentuali minime di armatura trasversale e longitudinale indicate dalla normativa, la rotazione limite di collasso θu, deve essere ridotta in ragione di un fattore 0.85 [Ntc18-C8.7.2.3.2, Istruzioni Ntc08-C8F.1, Opcm 3274-11.A.1].

Questa disposizione può essere rispettata a livello di singolo elemento, in quanto il programma permette di impostare il fattore riduttivo direttamente nella sezione tipo dell'elemento (vedi fogli Sezioni travi, pilastri e pareti). 

Riduzione per carenza di confinamento

Nel caso la staffatura dell'elemento resistente sia carente negli ancoraggi terminali, un'eventuale apertura della staffa prima che questa raggiunga la sua resistenza di calcolo pregiudica sensibilmente la sua capacità di fornire confinamento. In questi casi, l'effetto di confinamento può essere annullato, secondo le indicazioni della normativa [Ntc18-C8.7.2.3.2, Istruzioni Ntc08-C8F.1, Opcm 3274-11.A.1] o comunque ridotto tramite un fattore riduttivo da applicare al parametro α che esprime l'efficienza del confinamento. Anche questa disposizione può essere rispettata a livello di singolo elemento, in quanto il programma permette di impostare il fattore riduttivo direttamente nella sezione tipo dell'elemento (vedi fogli Sezioni travi, pilastri e pareti). 

Espressione alternativa per la rotazione al collasso

A titolo informativo si riporta anche una espressione alternativa per la rotazione al collasso, non utilizzata nella presente versione del programma:

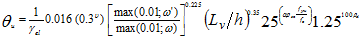
Per i riferimenti di normativa vedi: [Ntc18-C8.7.2.3.2, Istruzioni Ntc08-C8F.1, Opcm 3274-11.A.1].


in cui:

Lv         luce di taglio, ovvero distanza fra la sezione di estremità e quella a momento nullo,

γel         fattore riduttivo di duttilità (pari a 1.5 per elementi primari e ad 1.0 per elementi secondari),

b h         base ed altezza della sezione,

υ         sforzo assiale normalizzato di compressione                                 υ = N/(Acfc)

ω        percentuale meccanica di armatura longitudinale in trazione                ω = Asfy/(b h fc)

ω’        percentuale meccanica di armatura longitudinale in compressione                ω’ = A’sfy/(b h fc)

fc        resistenza a compressione del calcestruzzo,

fy        resistenza a snervamento dell’acciaio longitudinale,

fyw        resistenza a snervamento dell’acciaio trasversale,

ρsx        percentuale di armatura trasversale                ρsx = nb Ast /bo sh

sh        interasse delle staffe nella zona critica,

nb         numero di bracci staffe,

Ast        area trasversale del tondino staffa,

sh        interasse delle staffe nella zona critica,

ρd        percentuale di eventuali armature diagonali,

α        fattore di efficienza del confinamento (già definito precedentemente):