Contributo stabilizzante di muri e paratie
I muri e le paratie posizionati sul pendio danno un contributo alla stabilità in quanto in linea generale producono
- un contributo di attrito sulla superficie di scivolamento per effetto del loro peso proprio;
- un contributo di spinta per effetto dell’interazione opera e terreno in movimento.
Contributo di attrito
Se la la superficie di scorrimento non interseca l’intervento, il contributo stabilizzante è unicamente dovuto all’incremento della tensione tangenziale di attrito. Infatti, per effetto del peso proprio dell’intervento si ha un incremento ΔN della forza normale agente sulla base della striscia, e quindi un incremento Δtf della tensione tangenziale pari a:
Δtf = ΔN tg φ
Contributo di spinta
Nel consolidamento di pendii sono frequentemente usati interventi strutturali, come muri e paratie, capaci di intercettare forze instabilizzanti all’interno del corpo in frana e trasferirle al sostrato stabile, posto al di sotto della superficie di scivolamento.
Se la superficie di rottura non interseca l’opera, il meccanismo di interazione non si crea e non si ha nessun contributo di spinta.
Se invece l’opera attraversa tutta la massa in movimento e raggiunge il terreno stabile al di sotto della superficie di rottura, per effetto degli spostamenti orizzontali del terreno, si desta sull’opera una spinta dovute alle forze laterali trasmesse dal terreno. La valutazione di queste forze riconduce allo studio dell’interazione fra opera e pendio in frana ed è un problema affrontato da diversi autori (Broms, Viggiani, Ito & Matsui, De Beer & Carpenter, Fukuoka, Poulos, et al.).
Nel presente programma si propone una metodoligia di valutazione della spinta basata sull’analisi dei meccanismi di collasso locale che tipicamente possono verificarsi in queste situazioni, con riferimenti ai lavori teorici degli autori sopracitati.
In particolare sono considerati le quattro situazioni limite:
- crisi da scorrimento dell’opera,
- crisi da ribaltamento dell’opera,
- crisi da rottura del fronte spingente,
- crisi da tranciamento dell’opera,
che consentono di stimare con buona approssimazione valori limiti superiori della spinta offerta dall’intervento, in opposizione allo scorrimento del pendio.
Il valore di calcolo della spinta, cioè il valore realmente messo in conto nell’analisi, si assume infine come il valore minore registrato nei quattro casi limite, opportunamente ridotto mediante il coefficiente di sicurezza fsic assegnato in input, per l’opera in esame.
In particolare, la spinta di calcolo S si ottiene dalla seguente relazione:
S = min(Sls, Slr, Slf, Slt)/fsic
in cui
Sls è la spinta limite di scorrimento,
Slr è la spinta limite di ribaltamento,
Slf è la spinta limite di rottura fronte,
Slt è la spinta limite di tranciamento.
Le ipotesi semplificative adottate nell’analisi di tali meccanismi di crisi si accordono col livello delle approssimazioni insite in tutto il processo di modellazione e di analisi, di cui si è già discusso nei paragrafi precedenti. Si suppone, in particolare, che la spinta offerta dall’intervento strutturale sia orizzontale e applicata ad un terzo dell’altezza utile del fronte di spinta. Altre ipotesi sono assunte per le distribuzioni tensionali nell’intorno dell’intervento, assumendo andamenti costanti o lineari, corrispondenti a condizioni di plasticizzazione o a situazioni di spinta passiva esprimibili secondo la formula di Rankine o di Bell.
Contributo di spinta per i muri
Analizziamo con maggiore dettaglio le situazioni limite di lavoro per il caso dei muri.
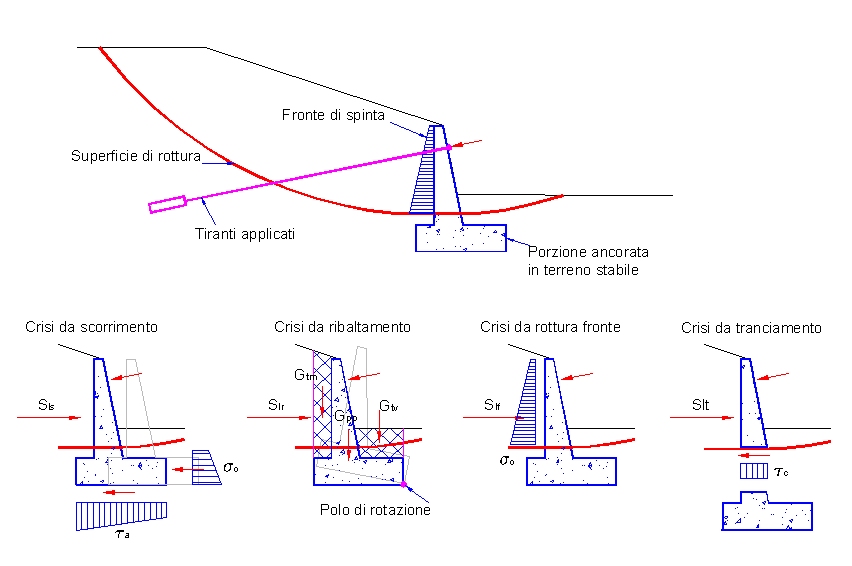
Meccanismo di crisi da scorrimento
Nel meccanismo di crisi da scorrimento si suppone che alla base del muro siano mobilitate delle tensioni tangenziali di attrito e una distribuzione di tensioni orizzontali sul fronte di valle della porzione ancorata in terreno stabile. Le tensioni tangenziali di attrito alla base del muro si suppongono distribuite con legge lineare e sono valutate in funzione delle tensioni effettive presenti agli spigoli di monte e di valle.
La distribuzione di tensioni orizzontali sul fronte di valle, anch’essa espressa con legge lineare, è valutata applicando la formula di Bell per il caso di spinta passiva:
so = sv tg2(45+f/2) + 2c tg(45+f/2)
La spinta Sls corrispondente al meccanismo di crisi per traslazione si ottiene quindi dall’equilibrio orizzontale con le forze resistenti, che in particolare sono la risultante delle tensioni tangenziali di attrito, la risultante delle tensioni passive orizzontali sul fronte valle e l’azione dei tiranti applicati.
Meccanismo di crisi da ribaltamento
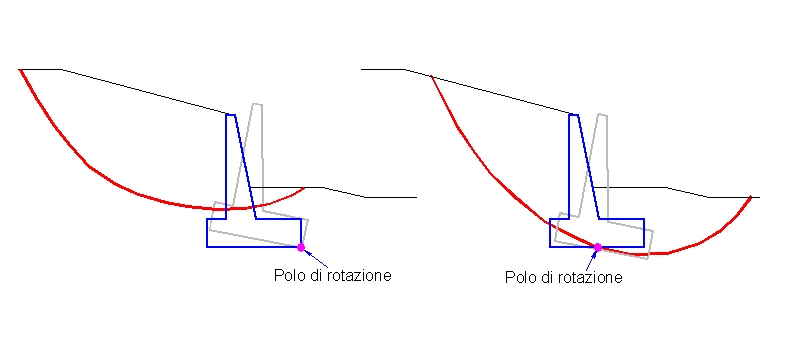
La spinta utile Slr per questo meccanismo di crisi si ottiene dall’equilibrio alla rotazione fra le forze agenti sul muro. Interviene in particolare il peso proprio del muro, le azioni dei tiranti applicati e il peso del terreno gravante sulla suola di fondazione. Il polo di rotazione si assume coincidente con lo spigolo inferiore di valle della porzione di muro collocata in terreno stabile. Se la superficie di rottura dovesse tagliare la suola di fondazione, il polo di rotazione arretra verso monte e si posiziona sulla linea di taglio con la superficie di rottura.
Meccanismo di crisi da rottura fronte
La spinta utile Slf è definita da meccanismi di crisi che si possono verificare sul fronte dell’opera direttamente investito dalla massa in scivolamento. Nel caso del muro questa viene valutata come risultante delle tensioni orizzontali agenti sul fronte, nell’ipotesi di stato passivo.
Meccanismo di crisi da tranciamento
La spinta utile Slt al limite del tranciamento si ottiene valutando l’area della sezione di muro tagliata dalla superficie di rottura e supponendo che su tale area si mobiliti la tensione tangenziale di rottura, caratteristica del materiale che costituisce il muro.
Contributo di spinta per le paratie
In maniera analoga al caso dei muri, anche per le paratie la spinta stabilizzante di calcolo viene valutata considerando quattro diversi meccanismi semplificati di collasso, corrispondenti a possibili situazioni di crisi dell’opera, ed assumendo come spinta di calcolo S il valore minimo, ulteriormente ridotto tramite il coefficiente di sicurezza assegnato.
Analizziamo con maggiore dettaglio le situazioni limite di lavoro per il caso delle paratie.
Paratie continue e discontinue
I valori meccanici che intervengono nel calcolo, come i pesi o la spinta resistente, sono sempre riferiti alla striscia di pendio di larghezza unitaria (1 metro). Nel caso di paratia discontinua, costituite da pali posti ad un determinato interasse, interviene quindi un fattore riduttivo fri che tiene conto della densità dei pali in direzione ortogonale alla sezione stratigrafica.
Meccanismo di crisi da scorrimento
Nel meccanismo di crisi da scorrimento si suppone che alla base della paratia siano mobilitate delle tensioni tangenziali di attrito e una distribuzione di tensioni orizzontali sul fronte di valle della porzione ancorata in terreno stabile. Le tensioni tangenziali di attrito alla base della paratia si suppongono distribuite con legge lineare e sono valutate in funzione delle tensioni effettive presenti agli spigoli di monte e di valle.
La distribuzione di tensioni orizzontali sul fronte di valle, anch’essa espressa con legge lineare, è valutata applicando la formula di Bell per il caso di spinta passiva:
so = sv tg2(45+f/2) + 2c tg(45+f/2)
La spinta Sls corrispondente al meccanismo di crisi da scorrimento si ottiene quindi dall’equilibrio orizzontale con le forze resistenti, che in particolare sono la risultante delle tensioni tangenziali di attrito, la risultante delle tensioni passive orizzontali sul fronte valle e l’azione dei tiranti applicati.
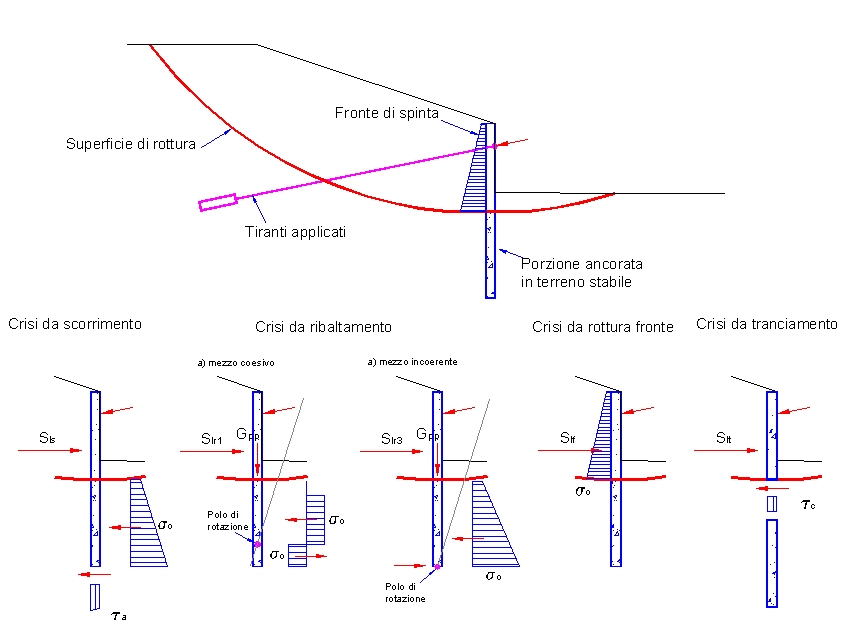
Meccanismo di crisi da ribaltamento
La spinta utile Slr per questo meccanismo di crisi si ottiene dall’equilibrio alla rotazione fra le forze e le tensioni del terreno agenti sulla paratia. Si utilizza in questo caso la teoria del Broms, basata sull’applicazione dei teoremi dell’analisi limite, nell’ipotesi che il palo sia libero di ruotare in testa e supponendo che la crisi sopravvenga per la plasticizzazione del terreno, piuttosto che per rottura strutturale (meccanismo di palo corto). Intervengono nel bilancio il momento della spinta, applicata ad un terzo del fronte di spinta, il momento delle forze dovute ai tiranti e il momento delle tensioni orizzontali, che si sviluppano lungo il fusto infisso in terreno stabile.
Vengono trattati separatamente i casi di mezzo puramente coesivo e di mezzo incorente e si assume come spinta limite il risultato maggiore fra i due casi, cioè :
Slf = max(Slr1, Slr2)
in cui
Slr1 è la spinta limite considerando il solo contributo coesivo,
Slr2 è la spinta limite considerando il solo contributo d’attrito.
Caso del mezzo puramente coesivo
In questo caso, il Broms fa l’ipotesi, confortata da risultanze sperimentali, che la reazione del terreno, in condizioni limite, sia nulla fino alla profondità di 1,5 B e poi costante con valore pari a 9cuB, in cui B è il diametro del palo e cu è la coesione non drenata. Il polo di rotazione si assume posto ad una certa profondità. Il palo ruota rigidamente attorno a tale punto, producendo un campo tensionale limite come quello riportato in figura.
Dagli equilibri alla traslazione ed alla rotazione si possono ricavare le incognite del problema, fra cui il valore della spinta limite.
Caso del mezzo puramente incoerente
In questo caso, il Broms fa l’ipotesi che la reazione del terreno, in condizioni limite, sia nulla al piano campagna e crescente linearmente con la profondità, con la legge 3Kpgz. In pratica questa distribuzione corrisponde alla spinta passiva di Rankine, amplificata con un fattore 3, per compensare le ipotesi semplificative insite nell’assunzione del coefficiente Kp.
Si ipotizza, inoltre, che il polo di rotazione coincida con la punta del palo. Questa assunzione si verifica con buona approssimazione e consente di semplificare il problema sostituendo alla reazione distribuita al di sotto del punto di rotazione una forza concentrata passante per la base del palo. In queste condizioni, il valore della spinta limite si può ricavare dal solo equilibrio alla rotazione.
Meccanismo di crisi da rottura fronte
La spinta utile Slf è definita da meccanismi di crisi che si possono verificare sul fronte dell’opera direttamente investito dalla massa in scivolamento. Per le paratie continue la valutazione della spinta è analoga a quelle per i muri. Nel caso di paratie discontinue, si assume la teoria di Broms per la fila di pali, che tiene conto della possibilità di rottura del terreno compreso fra due pali e quindi dell’inefficacia progressiva dell’effetto arco al crescere dell’interasse. In ogni caso la spinta è sempre limitata dal valore limite ottenibile sulla paratia continua, dove comanda la rottura del terreno a monte.
Meccanismo di crisi da tranciamento
La spinta utile Slt al limite del tranciamento si ottiene valutando l’area della sezione di paratia tagliata dalla superficie di rottura e supponendo che su tale area si mobiliti la tensione tangenziale di rottura, caratteristica del materiale che costituisce la paratia.