Ediplin 3

Il foglio si apre scegliendo l’opzione di menù Dati|Generali.

Il foglio dei Dati Generali è strutturato a pagine, nelle quali è possibile definire i parametri generali di tipo strutturale e geotecnico del modello. Queste due sezioni principali sono poi articolate all'interno in dati di carattere generale e in dati relativi ad una particolare tipologia (plinto superficiale, pali e pozzetti).

Parametri geotecnici

Nella sezione dei parametri geotecnici si potrà selezionare la quota della falda, il metodo di calcolo del carico limite verticale (Vesic, Hansen, Terzaghi, Meyerhof), il metodo di calcolo delle tensioni limiti orizzontali negli strati (Vesic, Hansen, Terzaghi, Meyerhof, Mathlock-Reese, Broms, nel caso dei pali), il metodo di calcolo dei cedimenti (Semispazio elastico, Bowles), i fattori di sicurezza sui parametri geotecnici ed altro ancora. Se si desidera impostare in autonomia i valori geotecnici riguardanti la portanza (verticale ed orizzontale) e la costante di Winkler, si può selezionare l'opzione Autonomo nella lista dei metodi proposti. Supponiamo in questo caso di accettare l'impostazione predefinita, lasciando quindi tutti i parametri immutati. Nel caso particolare avremo quindi che il carico limite verticale dei pali sarà valutato dal programma in base al metodo di Hansen, mentre i parametri riguardanti la costante di Winkler orizzontale lungo l'altezza dei pali e i valori limiti della portanza orizzontale saranno valutati secondo le indicazioni di Mathlock e Reese.

Questa sezione contiene al suo interno tre pagine:

• Geotecnici Generali,
• Geotecnici per Plinto superficiale,
• Geotecnici per Plinto su pali.

Parametri geotecnici generali

In questa pagina troviamo i seguenti dati.

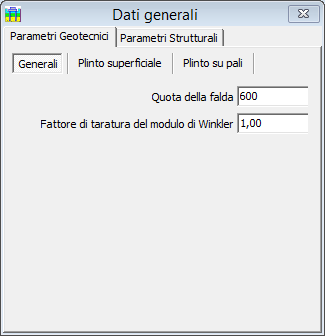
Quota della falda

Inserire la quota della falda [cm], riferita al piano campagna. L'assenza di falda, si esprime assegnando un valore alto in modo che i suoi effetti rimangano ininfluenti (ad esempio maggiore di 3-4 volte la dimensione del plinto superficiale o della profondità dei pali).

Fattore di taratura del modulo di Winkler negli strati

Quando il metodo di calcolo delle tensioni limiti orizzontali è impostato su uno dei metodi proposti (non quindi su Autonomo) il programma procede alla stima dei moduli di Winkler al variare della profondità, utilizzando una correlazione con la tensione limite proposta da Bowles

kw = qlim/2.54 [kg/cmc]

essendo:

kw        la costante di Winkler alla quota z,

qlim        il carico limite alla quota z [kg/cmq].

Il risultato di questa stima può essere influenzato dall'utente, tramite il fattore di taratura del modulo di Winkler richiesto in questa griglia, utilizzato come fattore aggiuntivo per il valore calcolato di kw:

valori >1        producono un incremento del valore finale,

valori <1        producono un decremento del valore finale.

Il valore predefinito del fattore di taratura è impostato ad 1.0, ininfluente sul risultato.

Per maggiori informazioni si veda il testo: “Bowles – Fondazioni – IV edizione - § 9.6”.

Parametri geotecnici per plinto superficiale

In questa pagina troviamo i seguenti dati.

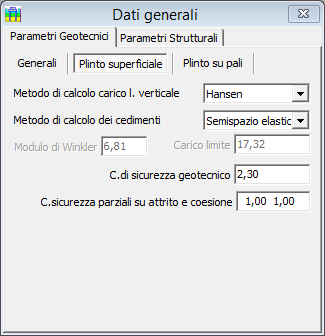
Metodo di calcolo del carico limite superficiale

Il programma consente di valutare il carico limite del plinto superficiale (nel caso non siano stati definiti pali) con metodi di tipo statico proposti da alcuni noti autori, oppure in alternativa, di assegnare autonomamente i valori di portanza, nel caso siano note da prove eseguite in sito o da altri indagini.

In particolare, le opzioni disponibili sono le seguenti:

• Autonomo,
• Vesic,
• Hansen,
• Terzaghi,
• Meyerhof.

Selezionando uno dei metodi proposti il programma procede al calcolo del carico limite e del modulo di Winkler per il plinto superficiale e ne riporta i valori in questa stessa tabella. Se invece si seleziona l'opzione Autonomo, questi stessi valori potranno essere riassegnati dall'utente.

Impostazione autonoma del carico limite superficiale e del modulo di Winkler

Quando si seleziona l'opzione "Autonomo" per il metodo di calcolo del carico limite, diventano attive le caselle per la digitazione diretta del carico limite e del modulo di Winkler. Negli altri casi, le caselle mostrano i valori ottenuti in automatico dal programma e non consentono la modifica del dato. In particolare:

nel caso il metodo sia impostato su Autonomo, l'utente può assegnare autonomamente i valori;

nel caso il metodo sia impostato su uno dei metodi disponibili, l'utente non può assegnare autonomamente i valori: il carico limite è ottenuto tramite  il metodo selezionato e il modulo di Winkler mediante la correlazione di Bowles (indicata al paragrafo precedente).

Metodo di calcolo dei cedimenti

La normativa dispone che per gli stati limite di esercizio vengano valutati i cedimenti e le distorsioni angolari in fondazione dovuti all'assestamento del terreno per effetto dei carichi trasmessi dalle fondazioni. I valori delle deformazioni così valutate devono risultare compatibili con la fruibilità dell'opera e con la sicurezza strutturale. Il controllo presuppone da un lato la definizione dei valori ammessi, per i quali si può fare riferimento a tabelle euristiche di letteratura, dall'altro il calcolo dei cedimenti, secondo il metodo selezionato in questo foglio. Le opzioni disponibili sono:

Per il calcolo dei cedimenti il programma prevede i due metodi:

• il metodo del semispazio elastico,
• il metodo di Bowles.

Il metodo del semispazio elastico

Il metodo assume che per il terreno valga la teoria dell'elasticità e quindi sia applicabile la soluzione  di Boussinesq (1885) che consente di ottenere la tensione verticale in un punto qualsiasi del semispazio elastico per una forza applicata in superficie. In genere la soluzione è considerata accettabile ai fini tecnici anche in presenza di terreni stratificati.

In letteratura esistono anche soluzioni derivate per integrazione da quella di Boussinesq, per trattare i casi di carico distribuito su superficie di una data forma.

Una volta nota la distribuzione delle tensioni nel mezzo, si può ottenere il cedimento in un punto integrando le deformazioni verticali lungo la verticale passante per il punto, fino ad una profondità significativa, che in genere è commisurata alla dimensioni dell'area caricata superficiale o delimitata dal raggiungimento di uno strato compatto:

in cui:

s        cedimento,

σ        tensione verticale nel terreno variabile con la profondità,

H        profondità del volume significativo o zona attiva,

E        modulo elastico del terreno.

Ai fini pratici la procedura viene eseguita discretizzando il terreno in un certo numero di strisce orizzontali e valutando l'integrale come sommatoria dei contributi delle singole strisce.

Il metodo di Bowles per plinti supeficiali

Il metodo proposto da Joseph E. Bowles (1) assume che il cedimento immediato possa ottenersi in base alla soluzione del carico distribuito su un semispazio elastico (2), secondo la seguente espressione:

in cui:

s                cedimento del terreno al piano di posa

q0 = N/Ap        carico distribuito sul terreno, essendo

               N        sforzo verticale totale applicato sull'elemento di fondazione,

               Ap         area di base dell'elemento di fondazione,

B, L                dimensioni minima e massima dell'elemento di fondazione,

B', L'                dimensioni minima e massima rivalutate in base al punto di valutazione:

               B' = B/2        L' = L/2        per il centro,

               B' = B                L' = L                per gli spigoli,

H                profondità d'influenza effettiva (effective influence depth), ovvero

               profondità significativa per la valutazione dei cedimenti, ovvero

               spessore dello strato compressibile con incrementi tensionali non trascurabili:

               H = min(5 B, Hsr)

               in cui Hsr è la profondità del primo strato rigido, ovvero con E > 10 Estrato superiore

μ                modulo di Poisson (valore consigliato μ = 0.35),

m                fattore numero di spigoli dipendenti dal punto scelto per la valutazione:
               m=1                se il cedimento è calcolato in uno spigolo,

               m=2                se il cedimento è calcolato nel punto medio di un lato,

               m=4                se il cedimento è calcolato nel centro della fondazione,

IS                fattore di forma, ottenibile dall'espressione:

               

               in cui:

               I1, I2, sono i fattori di forma di Steinbrenner (1934), dati da:

       

               essendo:

               M = L'/B'        N = H/B'

IR                 fattore riduttivo per rigidezza fondazione,

               IR = 1.0        per fondazione flessibile,

               IR = 0.97        per fondazione rigida,

IF                 fattore di profondità di Fox (1948), essendo IF ≤ 1.0, che rappresenta un importante effetto riduttivo per il calcolo del cedimento,

dipendente dalla profondità del piano di posa, dalle dimensioni della fondazione, e dal modulo di Poisson,

valutabile secondo la formula originaria di Fox (3), piuttosto complessa,

o in altenativa da tabelle, grafici ed espressioni di uso più operativo ottenute con tecniche di regressione (4),

Es                 modulo elastico del suolo alla profondità H, ottenibile come media pesata dei moduli elastici fino alla profondità H:

               

               per i singoli strati i valori possono essere ricavati con le correlazioni:

               STP:        Es = 500 (Ni,STP+15)  [kN/m2]

                       in cui Ni,STP è il n. medio di colpi fornito dalla prova allo strato i,

               CPT:        Es = (2..6) qc         se OCR ≈1

                       Es = (2..6) qc         se OCR>1)

                       in cui qc è la resistenza alla punta fornita dalla prova,

               su:        Es = (100..500) su,        se IP>30 (terreno plastico),

                       Es = (500..1500) su         se IP<30 (terreno poco plastico o rigido),

                       in cui su è la resistenza non drenata,

               Correzione per terreni sovraconsolidati:

                       Es OCR = Es sqrt(OCR)

1. Joseph E. Bowles, Foundation analysis and design, Fifth Edition, §5.6 Immediate settlement computations
2. Timoshenko and Goodier, Theory of elasticity, 124.Load distributed over a part of the boundary of a of semi-infinite solid
3. Fox E N. The mean elastic settlement of a uniformly loaded area at a depth below the ground surface. In: Proceedings of the Second International Conference on Soil Mechanics and Foundation Engineering. Rotterdam, 1948, 129–132
4. Mittal, Rawat e Bansal - Multivariable regression model for Fox depth correction factor

Coefficiente di sicurezza geotecnico sulla portanza

In questa stessa pagina è possibile inoltre definire il coefficiente di sicurezza da applicare al carico limite, per ottenere la portanza di calcolo. Si noti che al variare della normativa di calcolo, il programma propone un valore in accordo con le disposizioni in materia, che riportiamo sinteticamente di seguito, per cui l'utente nella maggior parte dei casi non deve digitare alcun valore, a meno che non ci sia la necessità di impostare valori differenti.

Valori regolamentari per il fattore di sicurezza sul carico limite superficiale:

Fs = 3,0 per Ntc96                        (per combinazioni di carico a coefficienti unitari),
Fs = 2,3 per Ntc08/Ntc18/EU        (secondo l'Approccio 2, per combinazioni di carico Slu).

Coefficienti di sicurezza parziali su attrito e coesione

E' possibile assegnare i coefficienti di sicurezza:
fga                Coefficiente parziale di sicurezza geotecnico su contributi di attrito,
fgc                Coefficiente parziale di sicurezza geotecnico su contributi di coesione,
che intervengono nel calcolo del carico limite, quando siano assegnati con valori maggiori dell'unità.
Questi fattori corrispondono ai fattori sui parametri geotecnici M1 (come indicato in Ntc08/Ntc18), che nei contesti di verifica secondo l'Approccio 2, si assumono tipicamente di valore unitario.

Parametri geotecnici per plinto su pali

I dati presenti in questa pagina sono i seguenti.

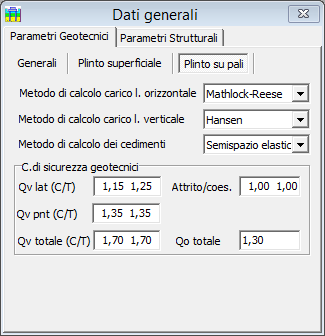
Metodo di calcolo del carico limite orizzontale

Il programma valuta il carico limite orizzontale dei pali secondo la teoria di Broms, tenendo conto della resistenza a rottura del palo a flessione e della resistenza del terreno alla spinta orizzontale. Per quest'ultimo aspetto, vari autori (fra cui lo stesso Broms) hanno proposto dei modelli che permettono di valutare la distribuzione della tensione limite orizzontale resistente del terreno lungo il fusto del palo che, opportunamente ridotta dal fattore di sicurezza impostato, interviene nelle procedure di calcolo della portanza orizzontale.

In questo foglio, l'utente può selezionare il metodo per la valutazione delle tensioni limite orizzontali, scegliendo fra le seguenti opzioni:

• Autonomo,
• Vesic,
• Hansen,
• Terzaghi,
• Meyerhof,
• Mathlock-Reese,
• Broms.

In base al metodo selezionato il programma determina la distribuzione lungo la profondità della tensione limite orizzontale e del modulo di Winker e orizzontale, riportanto i valori di riferimento nella griglia Dati|Stratigrafia (mostrata nella seguente figura), in corrispondenza dell'interfaccia fra gli strati:

tensione limite orizzontale                        colonna qlo,

modulo di Winkler orizzontale                         colonna kwo,

incremento di qlo per ml di profondità        colonna iq,

incremento di kwo per ml di profondità        colonna ik.

In alternativa, selezionando l'opzione "Autonomo", i valori qlo e kwo potranno essere definiti autonomamente dall'utente, tramite digitazione diretta nella griglia menzionata.

Metodo di calcolo del carico limite verticale

Il programma consente di valutare il carico limite dei pali con metodi di tipo statico proposti da alcuni noti autori. In alternativa, selezionando la relativa opzione, è possibile assegnare autonomamente i valori di portanza, nel caso siano note da prove eseguite in sito o da altri indagini.

In particolare, le opzioni disponibili sono le seguenti:

• Autonomo,
• Vesic,
• Hansen,
• Terzaghi,
• Meyerhof.

Selezionando uno dei metodi proposti il programma procede nella fase iniziale dell'analisi al calcolo dei valori di portanza a compressione e a trazione dei pali col metodo selezionato e mostra i risultati nella griglia Calcolo|Verifiche di portanza pali, alle colonne

Qcd        Portanza di progetto a compressione [t],
Qtd        Portanza di progetto a trazione [t].

Se invece si seleziona l'opzione Autonomo, i valori di portanza a compressione Qcd e a trazione Qtd per ogni palo dovranno essere assegnati dall'utente, nella griglia già menzionata, facendo attenzione che in tali valori siano già inclusi gli effetti dei fattori di sicurezza.

I metodi previsti sono di tipo statico ed esprimono la capacità portante ultima come:

Qck = Qpk + Qlk -W        (a compressione)
Qtk = Qlk + W        (a trazione)

in cui:
Qck        è la capacità portante limite a compressione,
Qtk        è la capacità portante limite a trazione,
Qpk        è la capacità portante ultima di punta,
Qlk        è la capacità portante ultima laterale,
W        è il peso proprio del palo.

Le capacità portanti di calcolo si ottengono mettendo in conto i coefficienti di sicurezza assegnati in questo foglio:

flc        Coefficiente parziale di sicurezza su portanza laterale a compressione
fpc        Coefficiente parziale di sicurezza su portanza di punta a compressione
ftc        Coefficiente parziale di sicurezza su portanza totale a compressione
flt        Coefficiente parziale di sicurezza su portanza laterale a trazione
fpt        Coefficiente parziale di sicurezza su portanza di punta a trazione
ftt        Coefficiente parziale di sicurezza su portanza totale a trazione

Le espressioni delle capacità portanti di calcolo Qcd a compressione e Qtd a trazione sono quindi:

Qcd = (Qpk/fpc+ Qlk/flc)/ftc - W                capacità portante di calcolo a compressione
Qtd =  Qlk/(flt ftt) + W                        capacità portante di calcolo a trazione

Nel caso siano presenti strati con attrito negativo, gli effetti vengono inclusi nella portanza laterale, in particolare la portanza laterale a compressione subirà una riduzione, essendo in questo caso le forze di attrito concordi col carico e quindi da portare in detrazione nel calcolo della portanza, limitatamente agli strati interessati dall'attrito negativo. Nel caso della trazione, l'attrito negativo è in opposizione al carico agente e quindi, per i tratti interessati, ne viene considerato il contributo resistente.

Tenendo conto di questo e considerando che il peso proprio del palo è portato in detrazione dalla portanza a compressione e in addizione alla portanza a trazione, si ottengono valori di portanza riferiti alla testa del palo (portanze utili), da confrontare in termini omogenei con i corrispondenti valori agenti, riferiti anch'essi cioè alla testa del palo.

Coefficienti di sicurezza geotecnici

Nel caso di sistema normativo Ntc96 gli unici fattori da impostare con valori maggiori di uno sono i coefficienti si sicurezza sulla portanza totale, da assumere pari a 3 sia per la compressione che per la trazione.

Nel caso di sistema normativo Ntc08/Ntc18, le verifiche geotecniche di portanza sono eseguite agli stati limite ultimi (slu) secondo l'Approccio 2, convenzionalmente indicato nella normativa con la sigla A1+M1+R3 [punto 6.4.2.1], in cui A1 rappresenta la combinazione delle azioni per gli stati limite ultimi, M1 i coefficienti di sicurezza sui parametri geotecnici ed R3 i coefficienti di sicurezza sulla capacità portante. In questo approccio, i fattori di sicurezza sui parametri geotecnici, ovvero i fattori Fsa e Fsc, rispettivamente per i contributi di attrito e coesione, possono essere assunti con valore unitario. I fattori di sicurezza sulla portanza totale dipendono invece dal numero di verticali indagate (sondaggio con prelievo di campioni indisturbati, prove penetrometriche, ecc.) al fine di consentano di identificare le caratteristiche geotecniche del sottosuolo. All'aumentare delle verticali indagate i fattori di sicurezza possono assumere valori decrescenti.

Per quanto riguarda i fattori di sicurezza sulla capacità portante, riportiamo nelle seguenti tabelle le indicazioni di normativa a riguardo.

Fattori di sicurezza sulla portanza dei pali trivellati secondo Ntc08/Ntc18

Fattori di sicurezza sulla portanza dei pali trivellati secondo Ntc96

Coefficienti di sicurezza parziali su attrito e coesione

E' possibile assegnare i coefficienti di sicurezza:

fga                Coefficiente parziale di sicurezza geotecnico su contributi di attrito,

fgc                Coefficiente parziale di sicurezza geotecnico su contributi di coesione,

che intervengono nel calcolo dei contributi ultimi di punta e laterale Qpk e Qlk, quando siano assegnati con valori maggiori dell'unità.

Questi fattori corrispondono ai fattori sui parametri geotecnici M1 (come indicato in Ntc08/Ntc18), che nei contesti di verifica secondo l'Approccio 2, si assumono tipicamente di valore unitario.

Metodo di calcolo dei cedimenti

La normativa dispone che per gli stati limite di esercizio vengano valutati i cedimenti e le distorsioni angolari in fondazione dovuti all'assestamento del terreno per effetto dei carichi trasmessi dalle fondazioni. I valori delle deformazioni così valutate devono risultare compatibili con la fruibilità dell'opera e con la sicurezza strutturale. Il controllo presuppone da un lato la definizione dei valori ammessi, per i quali si può fare riferimento a tabelle euristiche di letteratura, dall'altro il calcolo dei cedimenti, secondo il metodo selezionato in questo foglio. Le opzioni disponibili sono:

Per il calcolo dei cedimenti il programma prevede i due metodi:

• il metodo del semispazio elastico,
• il metodo di Bowles.

Il metodo del semispazio elastico

Il metodo assume che per il terreno valga la teoria dell'elasticità e quindi sia applicabile la soluzione  di Boussinesq (1885) che consente di ottenere la tensione verticale in un punto qualsiasi del semispazio elastico per una forza applicata in superficie. In genere la soluzione è considerata accettabile ai fini tecnici anche in presenza di terreni stratificati.

In letteratura esistono anche soluzioni derivate per integrazione da quella di Boussinesq, per trattare i casi di carico distribuito su superficie di una data forma.

Una volta nota la distribuzione delle tensioni nel mezzo, si può ottenere il cedimento in un punto integrando le deformazioni verticali lungo la verticale passante per il punto, fino ad una profondità significativa, che in genere è commisurata alla dimensioni dell'area caricata superficiale o delimitata dal raggiungimento di uno strato compatto:

in cui:

s        cedimento,

σ        tensione verticale nel terreno variabile con la profondità,

H        profondità del volume significativo o zona attiva,

E        modulo elastico del terreno.

Ai fini pratici la procedura viene eseguita discretizzando il terreno in un certo numero di strisce orizzontali e valutando l'integrale come sommatoria dei contributi delle singole strisce.

Il metodo di Bowles per pali

Il cedimento è rappresentato dallo spostamento verticale in testa al palo, dato dalla somma dello spostamento alla punta più l'accorciamento elastico del palo per effetto della compressione:

       s = sa + spt                 [mm]

in cui:

sa        spostamento per deformazione assiale del palo, ottenibile integrando le deformazioni assiali        lungo la luce del palo:

       

spt        spostamento alla punta per il cedimento del terreno

               

in cui:

Δq = N/Ap         tensione normale valutata sullo sforzo verticale totale (applicato in testa)

               N        sforzo verticale totale applicato sul palo,

               Ap        area della sezione trasversale del palo,

D                diametro del palo,

μ                modulo di Poisson (valore consigliato μ = 0.35),

m IS                 fattore di forma (per s.circolare m IS = 1.0),

IF                 fattore di profondita di Fox  (IF ≤ 1.0),

               IF = 0.55        se L/D ≤ 5,

               IF = 0.50        se L/D > 5,

Es                 modulo elastico del suolo sotto la punta, ottenibile con le correlazioni:

               STP:        Es = 500 (NSTP+15)  [kN/m2]

                       in cui NSTP è il n. di colpi fornito dalla prova,

               CPT:        Es = (2..6) qc         se OCR ≈1

                       Es = (2..6) qc         se OCR>1)

                       in cui qc è la resistenza alla punta fornita dalla prova,

               su        Es = (100..500) su,        se IP>30 (terreno plastico),

                       Es = (500..1500) su         se IP<30 (terreno poco plastico o rigido),

                       in cui su è la resistenza non drenata,

               Correzione per terreni sovraconsolidati:

               Es OCR = Es sqrt(OCR)

F1                 fattore di riduzione per distribuzione sul fusto,

               F1 = 0.25        se la portanza laterale annulla il carico in punta:        PP ≤ 0,

               F1 = 0.50        se la portanza laterale riduce il carico in punta:        PP > 0,

               F1 = 0.75        se la portanza è prevalentemente di punta.

Parametri strutturali

Nella sezione dei parametri strutturali si imposteranno le condizioni ambientali (ordinarie, aggressive, molto aggressive), i diametri dei tondini da utilizzare, la classe del calcestruzzo e del ferro, attivare il calcolo dell'interazione cinematica sismica ed altro.

Parametri strutturali generali

In questa pagina troviamo i seguenti dati.

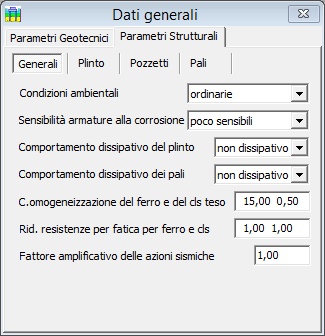
Condizioni ambientali

Si seleziona la condizione ambientale ai fini della durabilità del calcestruzzo e della protezione delle armature nei riguardi della corrosione, scegliendo una delle tre opzioni disponibili:

• ordinarie,                per classi di esposizione X0, XC1, XC2, XC3, XF1
• aggressive,        per classi di esposizione XC4, XD1, XS1, XA1, XA2, XF2, XF3
• molto aggressive, per classi di esposizione XD2, XD3, XS2, XS3, XA3, XF4.

Secondo le Ntc08 e Ntc18 la condizione ambientale da selezionare dipende dalla classe di esposizione del calcestruzzo, definite nelle Linee Guida per il calcestruzzo strutturale emesse dal Servizio Tecnico Centrale del Consiglio Superiore dei Lavori pubblici o nelle norme UNI EN 206/2006.
In particolare, le norme UNI EN 206/2006 classificano l'aggressività ambientale in 6 classi di esposizione (XO, XC, XD, XS, XF ed XA), ognuna delle quali è suddivisa in una o più sottoclassi ad aggressività crescente (vedi tabelle sul Manuale d'uso).

Per ogni classe viene riportata una descrizione sommaria dell'ambiente, alcuni esempi che aiutano ad inquadrare l'ambito e i valori che le norme citate richiedono di adottare, riguardanti il rapporto massimo acqua/cemento (a/c), la resistenza minima del calcestruzzo (cls) e il contenuto percentuale minimo in aria (aria).

Lo stato di aggressività ambientale limita le resistenze del calcestruzzo e condiziona le verifiche a fessurazione. In particolare, per quanto riguarda lo stato limite di fessurazione, questo è definito in base all’aggressività ambientale e alla sensibilità delle armature alla corrosione. Al crescere dell’aggressività ambientale si richiedono verifiche a fessurazione via via più impegnative, che a seconda dei casi possono consistere in:
verifiche di apertura fessure,
verifica di formazione fessure,
verifica alla decompressione.

Sensibilità delle armature alla corrosione

La sensibilità delle armature alla corrosione è funzione del tipo di armatura e in accordo con quanto riportato al punto 4.1.2.2.4 delle Ntc08, sono previsti due categorie di sensibilità:

• Poco sensibili        per acciai ordinari
• Sensibili                per acciai da precompressione.

Le usuali armature da carpenteria rientrano quindi nel primo caso, purché siano rispettati i valori minimi di copriferro.

In funzione dell’aggressività ambientale e della sensibilità delle armature alla corrosione, il programma imposta le verifiche a fessurazione secondo la norma selezionata, attivando i check delle verifiche nel foglio "Combinazioni: fattori parziali sulle resistenze" per il controllo della decompressione o dell’apertura delle fessure, in corrispondenza delle combinazioni di carico richieste ed assegnando i parametri di soglia. Le impostazioni sono eseguite secondo i prospetti combinatori riportati di seguito, in funzione della norma selezionata.

Quadro verifiche a fessurazione secondo Ntc18, Ntc08, Eurocodici

Quadro verifiche a fessurazione secondo Ntc96

Comportamento dissipativo di plinto e pali

Le recenti normative tecniche (Ntc08, Ntc18, Ec) richiedono che le strutture di fondazione di tipo superficiale siano progettate ipotizzando per esse un comportamento non dissipativo. In queste condizioni la capacità delle membrature è calcolata con riferimento al loro comportamento elastico o sostanzialmente elastico, che corrisponde a trascurare le capacità deformative dei materiali ferro e calcestruzzo, al di là del limite di prima plasticizzazione. Rientrano in questa casistica la struttura del plinto (sia esso superficiale o poggiato su pali) e le strutture di connessione con l'elevazione, quali i pozzetti per l'alloggiamento di pilastri prefabbricati. Per i pali si accetta invece sia il comportamento non dissipativo, sia quello dissipativo.

Nel presente foglio, l'utente può stabilire il comportamento dissipativo del plinto, comprendente anche gli eventuali pozzetti, e i pali. In effetti per i primi, la norma impone il comportamento dissipativo e, per tale ragione, la scelta è fissata all'opzione di comportamento non dissipativo. Per i pali invece ci sono entrambe le opzioni:

• comportamento non dissipativo: selezionando tale opzione il progetto farà riferimento a specifiche di progetto meno gravose (in termini di area di ferro e passo della staffatura), ma le verifiche a pressoflessione dovranno eseguirsi nell'ipotesi di comportamento sostanzialmente elastico;
• comportamento dissipativo: selezionando tale opzione il progetto dovrà prevedere zone a comportamento dissipativo, nelle quali dovranno essere rispettate specifiche di progetto più gravose (in termini di area di ferro e passo della staffatura), disposizioni di contenimento dello stato tensionale a taglio, a compressione e a p.flessione (Ntc18 §7.2.5), con la possibilità però di effettuare verifiche a pressoflessione mettendo in conto la piena capacità deformativa del calcestruzzo e del ferro. Deve essere prevista una zona dissipativa in testa al palo, estesa per una lunghezza almeno pari a 10 volte il diametro del palo.

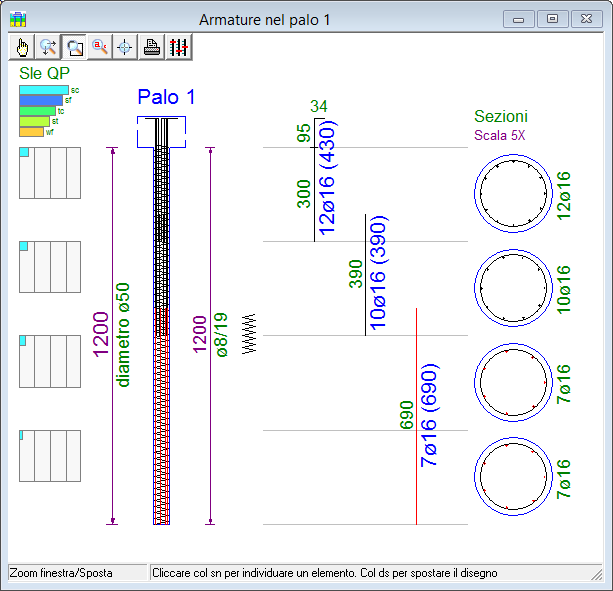
Armatura del palo per condizione non dissipativa, si nota una staffatura uniforme su tutta la luce

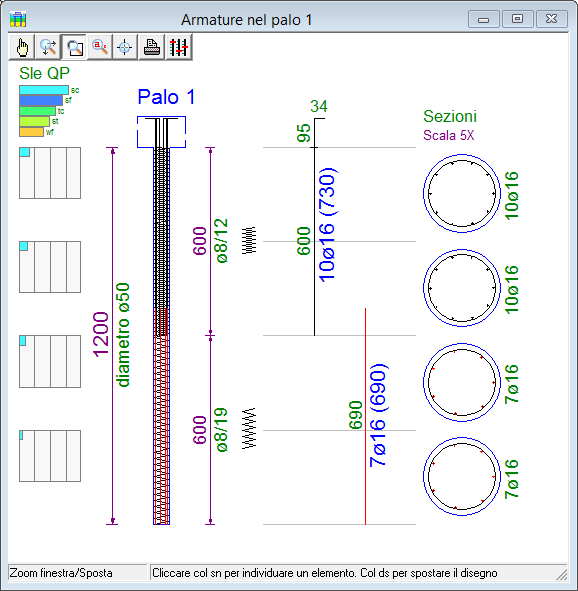
Armatura del palo per condizione dissipativa, si nota una doppia zona di staffatura

In particolare, le disposizioni di contenimento dello stato tensionale (come indicato in Ntc18 §7.2.5) consistono nel controllare che nelle zone dissipative siano verificate le seguenti prescrizioni:

capacità a taglio:                        Ta ≤ Tr/1.3

capacità a compressione:                σcm ≤ 0.45 fcd

capacità a p.flessione:                Ma ≤ 1.5 Mr                 (sic !)(*)

essendo:

Ta, Tr                 taglio agente e taglio resistente,

σcm, fcd           tensione agente media di compressione, resistenza di calcolo a compressione del calcestruzzo,

Ma, Mr                 momento agente e momento resistente.

(*) A riguardo dell'ultima disposizione, sarebbero opportune ulteriori precisazioni che ne possano chiarire meglio la significatività.

Coefficienti di omogeneizzazione

Sono richiesti i seguenti coefficienti di omogeneizzazione, definiti come rapporto fra il modulo elastico del materiale da omogeneizzare e il modulo elastico del calcestruzzo compresso:

• Coefficiente di omogeneizzazione del ferro,
• Coefficiente di omogeneizzazione del calcestruzzo teso

In genere si assumono valori convenzionali fissati da norme o da letteratura tecnica consolidata per tener conto di comportamenti non puramente elastici-lineari dei materiali.

Riduzione resistenze per fatica

Il dato consente di ridurre le resistenze nel ferro e nel calcestruzzo per tener conto di fenomeni di fatica.

Fattore amplificativo delle azioni sismiche

Come abbiamo già detto, le recenti normative tecniche (Ntc08, Ntc18, Ec) prevedono per le strutture di fondazione un comportamento essenzialmente non dissipativo, ma controbilanciano questa disposizione richiedendo l'incremento delle azioni agenti. In particolare si richiede  che gli scarichi provenienti dall'elevazione siano opportunamente amplificati (Ntc08/Ntc18 § 7.2.5, EC8 §4.4.2.6), in maniera da conferire agli elementi non dissipativi della fondazione un adeguato livello di sovraresistenza, nello spirito della gerarchia delle resistenze. Le norme propongono alcune opzioni alternative per ottenere questo risultato, ma fra queste quella che meglio si interfaccia con i valori di calcolo corrisponde ad amplificare le azioni sismiche trasmesse dall'elevazione mediante un fattore da assumere in accordo con le disposizioni della norma adottata, di cui riportiamo una sintesi nelle tabelle successive.

Si tenga presente che l'effetto è valutato nella fase d'inviluppo delle sollecitazioni, amplificando col fattore assegnato gli effetti delle azioni di carico sismiche, definite nel foglio Condizioni di carico per singole azioni e nel foglio collegato Carichi pilastri per condizione. Rimarchiamo il fatto che in questo contesto i valori delle forze e delle coppie assegnati nell'ultimo foglio citato non debbono includere alcun effetto di amplificazione, essendo questo applicato dal programma nella fase di inviluppo.

Per i carichi assegnati già combinati, nei fogli Condizioni di carico per azioni combinate e nel foglio collegato Carichi pilastri per azione combinata, l'effetto amplificativo deve invece essere incluso nei valori assegnati, naturalmente per quelle combinazioni che contengono l'azione sismica.

Disposizioni Ntc08/Ntc18 (§7.2.5)

Disposizioni EC8 (§4.4.2.6)

Parametri strutturali per il plinto

In questa pagina troviamo i parametri di progetto relativi al corpo del plinto.

 

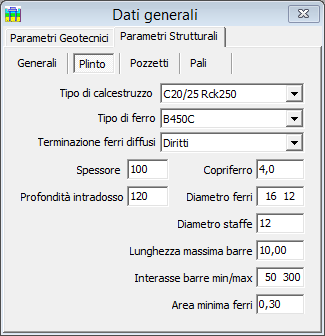
Tipo di calcestruzzo per il plinto

Assegnare il tipo di calcestruzzo, selezionandolo dalla lista a tendina.

Tipo di ferro per il plinto

Assegnare il tipo di ferro, selezionandolo dalla lista a tendina.

Terminazione ferri diffusi

Il parametro definisce la modalità di terminazione dei ferri diffusi, ovvero dei ferri disposti in maniera uniforme in due direzioni ortogonali su tutta l'area del plinto, per i due lembi (inferiore e superiore). Le opzioni disponibili nella lista a tendina sono:

• Diritti:        in questo caso i ferri non sono ripiegati in direzione verticale in corrispondenza del perimetro,
• Ripiegati:        in questo caso i ferri sono ripiegati in direzione verticale in corrispondenza del perimetro.

Terminazione ferri nei pozzetti

L'opzione definisce la modalità di chiusura della sagoma ferri dei pozzetti, selezionandola fra le due diverse alternative:

• Su un vertice
• Su due vertici

I ferri verticali ed orizzontali nei pozzetti hanno una forma rettangolare chiusa. Nel primo caso il ferro è chiuso in un solo vertice, dal quale è prolungato per il necessario ancoraggio con una piegatura a 135°. Nel secondo caso il ferro ha una sovrapposizione su uno dei lati più corti della sagoma e quindi viene ripiegato a 135° nei due vertici del lato sovrapposto.

Spessore del plinto

Definisce lo spessore del plinto, ovvero la dimensione nella direzione verticale, supposta uniforme su tutta l'area.

Profondità dell'intradosso del plinto

Definisce la profondità dell'intradosso del plinto, rispetto al piano campagna.

Copriferro nel plinto

Si assegna il copriferro dell'armatura del plinto.

Le Ntc96, al punto 6.1.4 del Dm 9/1/96, dispone che l'armatura resistente in solette, setti e pareti, debba distare almeno 0.8 cm dalla superficie esterna del conglomerato, da elevare comunque a 2 cm nel caso di ambiente aggressivo.

Le Ntc08 prevedono che il copriferro debba essere dimensionato in funzione dell'aggressività ambientale, della sensibilità alla corrosione delle armature e tenendo conto anche delle tolleranze di esecuzione. Nelle Istruzioni per l'applicazione delle Ntc08 (Circolare 617/09), al punto C4.1.6.1.3 è riportata la tabella C4.1.IV con i copriferri minimi da adottare in funzione dell'aggressività ambientale e della classe di resistenza del calcestruzzo, che riportiamo di seguito.

I valori della tabella si riferiscono a costruzioni con vita nominale di 50 anni. Per costruzioni con vita nominale di 100 anni i valori della tabella vanno aumentati di 10 mm. Per classi di resistenza inferiori a Cmin i valori della tabella sono da aumentare di 5 mm. Per produzioni di elementi sottoposte a controllo di qualità che preveda anche la verifica dei copriferri, i valori della tabella possono essere ridotti di 5 mm. Ai valori di tabella vanno aggiunte le tolleranze di posa, pari a 10 mm o minore, secondo indicazioni di norme di comprovata validità.

Diametri dei ferri nel plinto

Sono richiesti due diametri di ferro. Nel caso si volesse forzare l'uso di un solo diametro è possibile assegnare i due valori uguali.

Diametri staffe nel plinto

Si definisce il diametro del tondino per gli spilli verticali nel corpo del plinto

Lunghezza massima nominale delle barre nel plinto

Si assegnerà la lunghezza massima delle barre di armatura, espressa in metri e al netto degli ancoraggi. Si ricorda che, per esigenze commerciali, la lunghezza di taglio standard dei ferri disponibili è di 12 m.

Interasse dei ferri nel plinto

Si assegnano l'interasse minimo e massimo per i ferri del plinto.

Area minima dei ferri nel plinto

Si richiede il fattore fa che esprime l’area minima dei ferri in percento rispetto all’area di calcestruzzo per il plinto.

Parametri strutturali per i pozzetti

In questa pagina troviamo i parametri di progetto relativi ai pozzetti o bicchieri, per l'alloggiamento di pilastri prefabbricati.

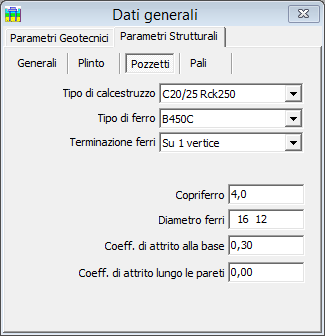
Tipo di calcestruzzo per i pozzetti

Assegnare il tipo di calcestruzzo, selezionandolo dalla lista a tendina.

Tipo di ferro per i pozzetti

Assegnare il tipo di ferro, selezionandolo dalla lista a tendina.

Terminazione ferri nei pozzetti

L'opzione definisce la modalità di chiusura della sagoma ferri dei pozzetti, selezionandola fra le due diverse alternative:

• Su un vertice
• Su due vertici

I ferri verticali ed orizzontali nei pozzetti hanno una forma rettangolare chiusa. Nel primo caso il ferro è chiuso in un solo vertice, dal quale è prolungato per il necessario ancoraggio con una piegatura a 135°. Nel secondo caso il ferro ha una sovrapposizione su uno dei lati più corti della sagoma e quindi viene ripiegato a 135° nei due vertici del lato sovrapposto.

Copriferro nei pozzetti

Si assegna il copriferro dell'armatura nei pozzetti. Vale quanto già detto per il copriferro del plinto.

Coefficiente di attrito alla base e lungo le pareti dei pozzetti

I due parametri esprimono i coefficienti di attrito rispettivamente alla base e lungo le pareti verticali del pozzetto, che intervengono nel calcolo delle forze agenti sulle pareti del pozzetto.

Per i pozzetti con pareti lisce (ovvero senza particolari accorgimenti di ingranamento) l'EC2 (§10.9.6.3) raccomanda di non superare il valore 0.3.

Parametri strutturali per i pali

In questa pagina troviamo i parametri di progetto relativi ai pozzetti o bicchieri, per l'alloggiamento di pilastri prefabbricati.

 

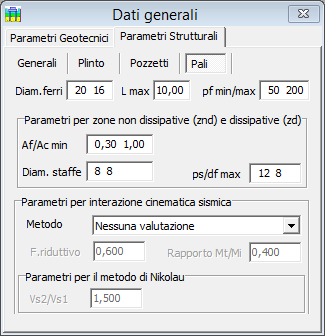
Diametri dei ferri nei pali

Sono richiesti due diametri di ferro. Nel caso si volesse forzare l'uso di un solo diametro è possibile assegnare i due valori uguali.

Diametri staffe nel plinto

Si definisce il diametro del tondino per gli spilli verticali nel corpo del plinto

Lunghezza massima nominale delle barre nei pali

Si assegnerà la lunghezza massima delle barre di armatura, espressa in metri e al netto degli ancoraggi. Si ricorda che, per esigenze commerciali, la lunghezza di taglio standard dei ferri disponibili è di 12 m.

Interasse dei ferri nei pali

Si assegnano l'interasse minimo e massimo per i ferri dei pali.

Area minima dei ferri nei pali

Sono richiesti i parametri che defiscono l'area di ferro minima nei pali in rapporto all'area di calcestruzzo, per i due casi di zona non dissipativa e zona dissipativa. Ricordiamo che la presenza di zone dissipative nei pali dipende dall'opzione selezionata per il comportamento dissipativo, trattata in un paragrafo precedente.

Per le zone dissipative le Ntc08 e Ntc18 al §7.2.5 dispongono che l'area di ferro sia almeno pari all' 1% dell'area di calcestruzzo.

Diametri staffe nei pali

Si definisce il diametro del tondino per la staffatura a spirale da disporre nei pali. Anche in questo caso sono richiesti due valori: il primo è riferito alle zone non dissipative, il secondo alle zone dissipative.

Per le zone dissipative le Ntc08 e Ntc18 al §7.2.5 dispongono che le staffe abbiano un diametro non inferiore a ∅8.

Limitazione del passo staffe in funzione del diametro dei ferri

Il parametro esprime il passo massimo delle staffe, rispettivamente per zone non dissipative e zone dissipative, in funzione del diametro minimo dei ferri longitudinali presenti. Per le zone dissipative le Ntc08 e Ntc18 al §7.2.5 dispongono che il passo staffe non superi il valore 8 df, essendo df il diametro dei ferri a flessione.

Metodo di calcolo degli effetti di interazione cinematica

La recente normativa italiana (Ntc08/Ntc18 §.7.11.5.3.2) richiede esplicitamente che in presenza di particolari circostanze venga condotta una valutazione degli effetti che si creano fra il palo e il terreno a causa della propagazione verticale delle onde simiche. Questo effetto viene detto di interazione cinematica e si sovrappone all'effetto, cosiddetto inerziale, dovuto alle forze trasmesse alla fondazione dalla sovrastruttura. In particolare, si raccomanda che l'analisi degli effetti cinematici nei pali siano valutate per costruzioni di Classe d'uso III e IV, per sottosuoli tipo D o peggiori, per valori di ag> 0,25g e in presenza di elevati contrasti di rigidezza al contatto tra strati contigui di terreno.

Secondo l'EC8 (En1998.5.2004 §5.4.2) i momenti flettenti dovuti all'effetto cinematico devono essere computati solo quando tutte le seguenti condizioni si presentano contemporaneamente: il terreno è di categoria D, S1 o S2, contiene strati consecutivi con brusce variazioni di rigidezza, la zona è di moderata o alta sismicità (ag S ≥ 0.10 g) e la sovrastruttura ha una classe d'uso di tipo III o IV.

Nel presente foglio l'utente può selezionare il metodo da utilizzare per la valutazione dell'effetto cinematico, che prevede le seguenti opzioni:

• Nessuna valutazione
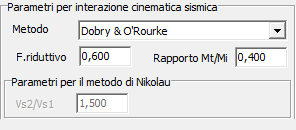
• Dobry R., O’Rourke
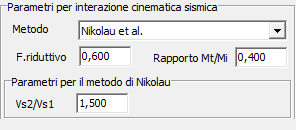
• Nikolaou et al.

Selezionando la prima opzione l'effetto cinematico non sarà valutato. Le due restanti opzioni rappresentano invece due dei metodi attualmente più usati per la valutazione di questo effetto e selezionandone una il programma eseguirà la valutazione dell'effetto cinematico, purche il sito ricada in zona sismica e siano presenti in stratigrafia almeno due strati.

Intuitivamente l'effetto cinematico corrisponde a quello che si avrebbe in un palo privo di sovrastuttura, immerso nel terreno, per effetto della propagazione verticale nel sottosuolo di onde di taglio. Il fenomeno dipende in maniera complessa dalla stratigrafia, dal comportamento non lineare del terreno, dagli effetti di smorzamento collegati e dall'entità delle deformazioni indotte dal sisma. In letteratura sono stati pubblicati svariati studi sull'argomento, nei quali sono state predisposte complesse modellazioni dinamiche agli elementi finiti, in campo lineare e non lineare. Essenzialmente però l'obiettivo rimane quello di tarare metodi semplificati in grado di quantificare l'effetto con una accuratezza sufficiente ai fini tecnici, considerato che un approccio rigoroso non è allo stato attuale proponibile al di fuori dell'ambiente accademico. In genere, si è visto che in linea generale l'effetto cinematico è trascurabile rispetto all'effetto inerziale, ovvero all'effetto dovuto all'oscillazione della sovrastruttura, a meno che non ci si trovi in circostanze particolari che tendono ad amplificare il fenomeno, quali ad esempio la presenza di un forte contrasto di rigidezza fra due strati di terreno successivi, una forte sismicità del sito, una classe di sottosuolo D o peggiore, che sono esattamente le condizioni indicate dalla normativa italiana e dagli Eurocodici.

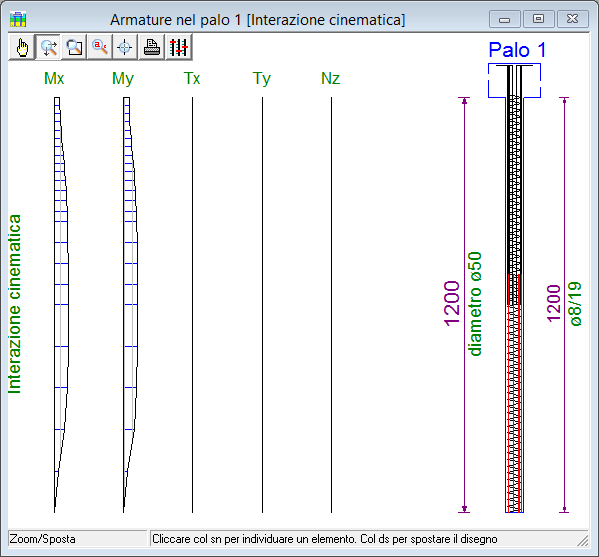
Per soddisfare questa esigenza, il programma precede i metodi di Dobry R., O’Rourke e di Nikolaou et al., che sono due dei più diffusi metodi semplificati attualmente disponibili. Entrambi i metodi consentono di ottenere il momento massimo M nel palo all'interfaccia fra due strati di diversa rigidezza, che sono individuati da programma in base al maggiore contrasto di rigidezza fra i moduli G del terreno. Una volta ottenuto il valore puntuale massimo, l'effetto è propagato ai fini delle verifiche su tutta la luce del palo, supponendo che il diagramma dei momenti sia espresso da una legge cubica e imponendo per esso il valore nullo alla punta del palo e una aliquota prefissata in testa al palo.

Si tenga presente che affinchè l'analisi di interazione cinematica venga eseguita è necessario:

selezionare il metodo di calcolo,

Fattore riduttivo

In entrambi i metodi, il momento Mi in corrispondenza dell'interfaccia fra i due strati a differente rigidezza viene ottenuto dalla relazione

in cui:

Mi(tr)         momento flettente nel palo in corrispondenza dell'interfaccia in regime transitorio (eccitazione sismica reale),

Mi(st)         momento flettente nel palo in corrispondenza dell'interfaccia in regime stazionario (eccitazione sismica armonica),

η        fattore riduttivo che consente di passare dal momento valutato per eccitazione sismica armonica al momento per eccitazione sismica reale.

Da vari studi condotti con accelerogrammi reali (Nikolaou e Gazetas, 1995, 2000) si è visto infatti che il momento valutato mediante una eccitazione sismica armonica stazionaria è in generale una stima in eccesso (anche 4 volte maggiore) del momento che si desta per terremoti reali di natura transitoria. Per ridurre questo effetto, gli autori hanno proposto la formula indicata precedentemente, nel quale il fattore riduttivo η varia nella maggior parte dei casi da 0.2 a 0.7, secondo le evidenze finora raccolte. L'utente ha in questo foglio la possibilità di assegnare il fattore riduttivo, impostato al valore predefinito η=0.6 (generalmente  in sicurezza).

Rapporto Vs1/Vs2

Nel caso sia stato selezionato il metodo di Nikolaou, viene richiesto anche il rapporto fra le velocità delle onde di taglio nei due strati con maggiore contrasto di rigidezza.

Rapporto Mt/Mi

Come dicevamo prima, con questi metodi si ottiene il valore puntuale del momento, in corrispondenza dell'interfaccia fra i due strati con maggiore contrasto di rigidezza. Ai fini delle verifiche, nasce quindi l'esigenza di propagare l'effetto su tutta la luce del palo e nel programma questa operazione si esegue ipotizzando che il diagramma dei momenti sia espresso da una legge cubica e imponendo per esso il valore nullo alla punta del palo e una aliquota prefissata in testa al palo.

Con questo dato, l'utente stabilisce quindi il rapporto Mt/Mi, essendo Mt il momento in testa e Mi il momento all'interfaccia fra gli strati, ottenuto dal metodo selezionato. Considerato che il momento all'interfccia è anche il valore massimo lungo il fusto, dovrà risultare che Mt/Mi ≤ 1, il valore predefinito è impostato su 0.4.

Area minima dei ferri nei pali in testa e sul fusto
Sono richiesti due valori che esprimono l’area minima dei ferri in percento rispetto all’area di calcestruzzo per i pali: il primo riferito alla zona di testa, con estensione pari a 10 diametri, e il secondo alla restante lunghezza.
Le Ntc08 al punto 7.2.5 dispongono:
area ferro longitudinale per la zona di testa (estesa almeno 10 diametri) ≥ 1.0% Ac
percentuale di armatura longitudinale per la restante luce ≥ 0.3% Ac

Interasse fra le barre minimo/massimo nel plinto e nei pali
Sono richiesti i valori minimo e massimo delle barre di armatura rispettivamente per il corpo del plinto e per i pali.
In particolare il valore massimo è utilizzato per il calcolo del numero minimo di ferri da disporre nella sezione. Il valore minimo è utilizzato nei controlli a valle del progetto, per evidenziare le sezioni con interferri inferiori al valore minimo impostato.

Ampiezza limite delle fessure
Sono richiesti i valori limite dell’apertura fessure w1, w2 e w3 fissati dalla normativa.
Quando si cambia sistema normativo i dati sono reinizializzati ai valori richiesti dalla norma selezionata.

Norma di verifica per pozzetti
Per il progetto e la verifica dei pozzetti il programma consente di selezionare la norma da tenere come riferimento, selezionandola fra le due diverse opzioni:
Cnr 10025/84
Cnr 10025/98