Foglio dei Tipi di terreno
Il foglio si apre scegliendo la voce di menù Dati|Tipi di terreno.
Nel foglio si definiscono le caratteristiche dei tipi di terreno.
Nel proseguo i tipi definiti in questa griglia, potranno essere utilizzati per la definizione della stratigrafia, impostando per ogni strato il tipo di terreno corrispondente.
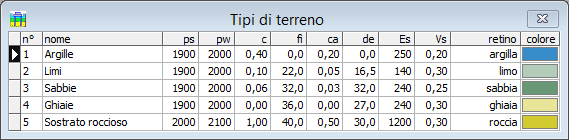
I dati richiesti sono:
nome breve descrizione del materiale (massimo 23 lettere),
ps peso secco [kg/mc],
pw peso saturo [kg/mc],
c coesione [kg/mq]
fi angolo di attrito [°]
ca adesione palo-terreno [kg/mq]
de angolo di attrito palo-terreno [°]
Es modulo elastico normale [kg/cmq],
Vs modulo di contrazione laterale di Poisson,
retino retino di visualizzazione,
colore colore di visualizzazione.
Pesi
Si richiedono i valori
ps peso del volume unitario del terreno secco (valore minimo),
pw peso del volume unitario del terreno saturo di acqua (valore massimo).
Coesione e angolo di attrito
La resistenza a taglio s di un cubetto di terreno è espressa secondo la relazione:
s = c + σ tan Φ in termini di sforzi totali,
s’ = c’ + σ tan Φ’ in termini di sforzi efficaci.
in cui:
σ, c, Φ sono lo sforzo verticale, la coesione e l’angolo di attrito in termini di sforzi totali,
σ’, c’, Φ’ sono lo sforzo verticale, la coesione e l’angolo di attrito in termini di sforzi efficaci.
La coesione dipende dai meccanismi di attrazione intermolecolare, mentre l’angolo d’attrito misura la resistenza dei granuli allo scorrimento relativo, per effetto dell’attrito.
Nel calcolo questi valori intervengono nella valutazione del carico limite dei pali. Il calcolo del carico limite è eseguito in termini di tensioni efficaci, si richiede pertanto che coesione ed angolo di attrito siano espressi in termini di sforzi efficaci.
Adesione ed angolo di attrito palo-terreno
L’adesione ca e l’angolo di attrito δ sono i due parametri che caratterizzano la resistenza tangenziale che si sviluppa sulla superficie laterale del palo e che produce il contributo di portanza lungo il fusto.
In particolare la resistenza tangenziale f viene calcolata come:
f = ca/Fsc + σ tan Φ /Fsa
in cui:
σo tensione orizzontale efficace, assunta in condizione di spinta passiva: σo = K o σv = (1-sin Φ) σv
Fsc Fsa fattori parziali di sicurezza per i contributi coesivi e di attrito assegnati (vedi paragrafo relativo ai Parametri geotecnici).
Sui valori da assumere, rileviamo in letteratura varie correlazioni, proposte con riferimento a casistiche particolari (pali trivellati/infissi, terreni coesivi/granulari, correlazioni ottenute da prove di carico/penetrometriche, ecc.). Considerata le differenti metodologie di approccio e la variabilità dei valori che si ottengono da tali correlazioni, ci è sembrato opportuno lasciare il controllo della modellazione all’utente, che potrà impostare i valori da considerare per ogni tipo di terreno.
Al riguardo il programma si limita alla impostazione dei valori predefiniti, in cui si assume:
ca = 0.5 c
δ = 0.75 Φ
Modulo elastico, coefficiente di Poisson
Sono proprietà elastiche che intervengono nella valutazione dei cedimenti di opere interagenti con i terreni, nell’ambito e nei limiti applicativi della teoria dell’elasticità.
Il modulo elastico E è definito come rapporto fra lo sforzo e la deformazione assiale. Può essere ricavato misurando la pendenza delle curve sforzi-deformazioni ottenute nel corso di prove triassiali o mediante prove in situ, come la SPT (Standard Penetration Test), la CPT (Cone Penetration Test) o altre.
Il coefficiente di Poisson μ è definito come il rapporto fra la deformazione assiale (di compressione) e la dilatazione trasversale. Il coefficiente può assumere valori negativi, quando si ha contrazione trasversale e valori positivi quando si ha dilatazione. Il valore μ = 0.5 rappresenta una deformazione senza aumento del volume.
Il campo di variabilità di μ per i terreni è in genere compreso fra -0.1÷ 1.0.
Il campo di variabilità di μ ammissibile con la teoria dell’elasticità è -1.0 ÷ 0.5.
Se si introduce il modulo di elasticità tangenziale G definito come rapporto fra lo sforzo di taglio e lo scorrimento angolare, la teoria dell’elasticità ci da una relazione che lega E, G e μ:
G = E/(2+2μ)
Valori indicativi del modulo elastico Es per terreni
Terreno |
Es [kg/cmq] |
Argilla molto molle |
20 ÷ 150 |
Argilla molle |
50 ÷ 250 |
Argilla media |
150 ÷ 500 |
Argilla dura |
500 ÷ 1000 |
Argilla sabbiosa |
250 ÷ 2500 |
Limo |
20 ÷ 200 |
Sabbia limosa |
50 ÷ 200 |
Sabbia sciolta |
100 ÷ 250 |
Sabbia compatta |
500 ÷ 800 |
Sabbia e ghiaia sciolta |
500 ÷ 1500 |
Sabbia e ghiaia compatta |
1000 ÷ 2000 |
Fonte: Bowles – Fondazioni – IV edizione
Valori indicativi del modulo di Poisson μs per terreni
Terreno |
μs |
Argilla satura |
0.4 ÷ 0.5 |
Argilla non satura |
0.1 ÷ 0.3 |
Argilla sabbiosa |
0.2 ÷ 0.3 |
Limo |
0.3 ÷ 0.35 |
Sabbia |
-0.1 ÷ 1.0 |
Sabbia ghiaiosa (comunemente usata) |
0.3 ÷ 0.4 |
Roccia |
0.1 ÷ 0.4 |
Fonte: Bowles – Fondazioni – IV edizione
